ответ: 1) думаю так
х-первое число
(х-2) - второе число
одз: x > 0
уравнение:
х·(х-2)=15
х²-2х-15 = 0
d=4-4·1·(-15)=4+60=64=8²
x₁ = - 3 < 0 не удовлетворяет одз
x₂ = 5 удовлетворяет одз
5 -первое число
5-2=3 - второе число
ответ: 5; 3
2) так
х м- одна сторона
(х-10) м - вторая сторона
6а = 600м²
одз: x > 0
уравнение:
х·(х-10)=600
х²-10х-600 = 0
d=100-4·1·(-600)=100+2400=2500=50²
x₁ = - 20 < 0 не удовлетворяет одз
x₂ = 30 удовлетворяет одз
30 м - одна сторона
30-10 = 20 м - вторая сторона
2·(30+20) = 100 м - периметр участка, которому должна равняться длина изгороди для дан�ого участка.
90м < 100м
ответ: 90м изгороди не хватит для данного участка.
3)так
количество линий связи равно с, числу сочетаний из n по 2:
n₁ = -7 < 0 отрицательное не удовлетворяет условию
n₂ = 8 удовлетворяет условию
ответ: 8.
4)
пусть x% - процент снижения в первый раз, тогда
х/2%=0,5х% - процент снижения во второй раз;
40: 100% · х% = 0,4х руб. - первая скидка
(40-0,4х) руб. - цена после первого снижения
(40-0,4х) : 100% · 0,5х% = (0,4-0,004х) · 0,5х = (0,2х-0,002х²) - вторая скидка
(40-0,4х) - (0,2х-0,002х²) = (40-0,6х-0,002х²) - цена после второго снижения
по условию цена товара после второго снижения равна 34р20к,
получаем уравнение:
40-0,6х-0,002х² = 34,2 (одз: 0%
0,002x²+0,6x-5,8=0
d=0,6²-4*0,002*5,8=0,3136=0,56²
x₁=10% удовлетворяет одз: 0%< 10%< 100%)
x₂=290% не удовлетворяет одз: 290%> 100%)
ответ: на 10%.
подробнее - на -
объяснение:
а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
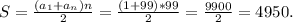
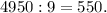
Так как получилось разделить нацело, то 1234...9899 делится на 9.
Отметь как лучший ответ