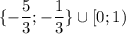Найдите все значения параметра а, при каждом из которых система (фото в закрепе) имеет 1 решение. с объяснением. ответ: а€ [0; 1) в объединении с {-5/3; -1/3}
Можно построить этот график. Учитывая неравенство, строим до прямой x = 6.
Рассмотрим второе уравнение:
График этого уравнения — прямая, проходящая через точку (6; 0) с меняющимся углом наклона. Причём из него же следует, что точку с y = 2 можно выколоть на графике первого уравнения.
График первого уравнения начерчен красным цветом, вариации второго — зелёным.
Возьмём a = 0 и будем увеличивать угол наклона. До a = 1 будет ровно одно пересечение. При a ≥ 1 прямая либо будет параллельна прямой y = x + 2, либо не будет иметь пересечений.
Если уменьшать угол наклона, то при отрицательных a будет два решения, за исключением случаев, когда прямая проходит через выколотую точку (0; 2) и "общую" точку (3; 5):
Пусть неизвестное целое число равно х, тогда х-1 и х+1 - целые числа, расположенные слева и справа от числа х, соответственно. По условию, сумма квадратов данных чисел равна 869. Составим уравнение: (х-1)²+х²+(х+1)²=869 х²-2х+1+х²+х²+2х+1=869 3х²+2=869 3х²=869-2 3х²=867 х²=867:3 х²=289 х= x=
1) x=17 x-1=17-1=16 x+1=17+1=18 Получаем, 16, 17 и 18 - три последовательных целых числа Проверка: 16²+17²+18²=256+289+324=869 2) х=-17 х-1=-17-1=-18 х+1=-17+1=-16 Получаем, -18, -17 и -16 - три последовательных целых числа Проверка:(-18)²+(-17)²+(-16)²=324+289+256=869
Формула цилиндра V=ПиR^2*H ПиR^2 это уже дано 4Пи , рассмотрим это с другой стороны , чтобы получить 4п по формуле площади основания ПиR^2 это надо чтобы радиус у цилиндра был 2 т.е. 2 в квадрате умножить на пи получаем 4п.Так вот теперь мы знаем что диаметр у нас 4 .Рассмотрим треугольник который состоит из осевого сечения и диаметра цилиндра нам надо найти высоту, чтобы посчитать по формуле объем цилиндра.Так вот в том треугольнике нам известна гипотенуза и снизу сторона. Считаем по теореме пифагора h^2=5^2-4^2 h^2=25-16 h=3 подставляем в формулу цилиндра V=пиR^2H V=Пи*4*3 V=12пи
Рассмотрим первое уравнение:
Можно построить этот график. Учитывая неравенство, строим до прямой x = 6.
Рассмотрим второе уравнение:
График этого уравнения — прямая, проходящая через точку (6; 0) с меняющимся углом наклона. Причём из него же следует, что точку с y = 2 можно выколоть на графике первого уравнения.
График первого уравнения начерчен красным цветом, вариации второго — зелёным.
Возьмём a = 0 и будем увеличивать угол наклона. До a = 1 будет ровно одно пересечение. При a ≥ 1 прямая либо будет параллельна прямой y = x + 2, либо не будет иметь пересечений.
Если уменьшать угол наклона, то при отрицательных a будет два решения, за исключением случаев, когда прямая проходит через выколотую точку (0; 2) и "общую" точку (3; 5):
При (0; 2)ответ: