7/12
Объяснение:
Заштрихованная фигура состоит из двух криволинейных трапеций. Одна, находящаяся над осью абсцисс, ограничена графиком y = x², двумя вертикальными прямыми x = -1 и x = 0, а также самой осью Ox. Вторая, находящаяся под осью абсцисс (из-за этого ее площадь возьмем со знаком минус), ограничена графиком y = x³, теми же вертикальными прямыми и той же осью Ox.
Тогда площадь S рассматриваемой фигуры будет равна сумме двух определенных интегралов (один — от x², другой — от x³ со знаком минус), оба вычисленных на отрезке [-1; 0]:
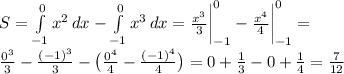
(см. объяснение)
Объяснение:
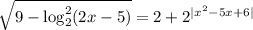
Введем функции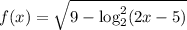 
и 
. Про вторую сразу скажем, что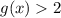 
, но на этом не остановимся. Видим, что в степени у нас модуль, а значит самое маленькое, что мы можем получить - это 
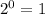при 
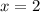или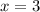 
. Тогда наименьшее значение этой функции будет равно 
.
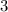Теперь разберемся с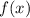 
. У нас есть квадратный корень, поэтому все значения функции точно 
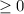. Но и здесь мы идем дальше. Поменяем временно 
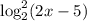на букву 
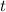. Тогда будет 
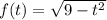. Под корнем парабола, ветви которой направлены вниз, а значит есть наибольшее значение, равное 
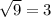при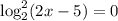 
, откуда .
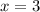Наибольшее значение 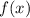равно 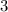и достигается при 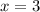. Наименьшее значение 
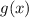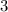равно и достигается пр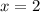и или .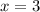
Тогда единственный корень исходного уравнения .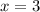
Уравнение решено!
y(-3)=-4.(-3)+1=12+1=13
y(-3)=13