Пусть  - канонический базис в
- канонический базис в 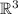 .
.
Тогда матрицу перехода 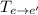 можно найти следующим образом:
можно найти следующим образом:
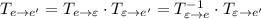
Если записать блочную матрицу 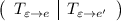 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 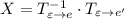
Матрицу 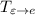 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 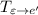 .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
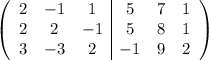
Вычтем первую строку из второй и третьей:
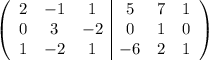
Вычтем из первой строки 2 третьих и поменяем их местами:
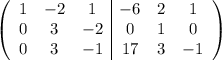
Вычтем из третьей строки вторую:
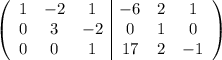
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
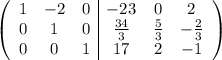
Прибавляем в первой строке 2 вторых:
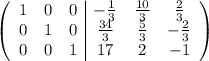
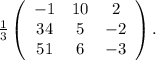
2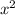 - х -
- х - 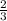 х = 0 , для обох прикладів
х = 0 , для обох прикладів
Объяснение:
Дивіться на формулу №1 на фото
У вас -b = 1, тобто b = -1
2а = 4, тобто а=2
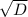 =
= 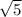 , тобто D=5
, тобто D=5
D= 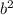 - 4*а*c ,
- 4*а*c ,
у вас ВСЕ відомо крім "с" , яке не важко знайти
5=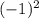 - 4*2*с
- 4*2*с
5=1-6с
6с=1-5
с=-4/6
с=-2/3.
Ваше рівняння.. підставляємо всі відомі коефіцієнти 2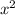 -х -
-х - 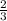 х = 0
х = 0
А ДРУГЕ рівняння - це теж саме квадратне рівняння.
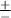 в ПЕРШій формулі вставленого фото означає що ваше рівняння графічно - звичайна ПАРАБОЛА, вона ДВІЧІ перетинає вісь ІКС. Тому і виходить ДВА ікса
в ПЕРШій формулі вставленого фото означає що ваше рівняння графічно - звичайна ПАРАБОЛА, вона ДВІЧІ перетинає вісь ІКС. Тому і виходить ДВА ікса 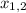 .
.
А ми, якщо ви не знаєте, рішаючи ці равняння як раз і шукаєто в яких точках цей графік перетне вісь ІКС.
За звичай рівняння дорівнює ІГРЕКУ. А у вас цей самий ІГРЕК дорівнює НУЛЮ (0) .
А якщо ІГРЕК дорівнює нулю, значить це і є вісь ІКСіВ.

16*8√3 = 128√3