Объяснение:
№1062
а)6х-4у=5
8х-3у=2
Умножим первое уравнение на -4, а второе на 3, чтобы решить систему методом алгебраического сложения.
Смысл метода алгебраического сложения в том, чтобы при сложении уравнений одно неизвестное взаимно уничтожилось. То есть, коэффициенты или при х, или при у были одинаковыми, но с противоположными знаками. Для того, чтобы этого добиться, преобразовывают одно из уравнений, как бы подгоняют ко второму, можно умножать обе части уравнения на одно и то же число, делить.
После умножения:
-24х+16у= -20
24х-9у=6
Складываем уравнения:
-24х+24х+16у-9у=6-20
7у= -24
у= -2
Теперь вычисленное значение у подставляем в любое их двух уравнений системы и вычисляем х:
6х-4у=5
6х-4*(-2)=5
6х+8=5
6х=5-8
6х=-3
х= -0,5
Решение системы уравнений х= -0,5
у= -2
б)12у+15х=8
16у+9х=7
Умножим первое уравнение на 3, а второе на -5, чтобы решить систему методом алгебраического сложения.
После умножения:
36у+45х=24
-80у-45х= -35
Складываем уравнения:
36у-80у+45х-45х=24-35
-44у= -11
у=1/4 (или 0,25)
Теперь вычисленное значение у подставляем в любое их двух уравнений системы и вычисляем х:
12у+15х=8
12*0,25+15х=8
3+15х=8
15х=8-3
15х=5
х=5/15=1/3
Решение системы уравнений х=1/3
у=1/4
№1064
а)5х-2=4(х+2у)-8
3(2х-у)+6=24у+12
5х-2=4х+8у-8
6х-3у+6=24у+12
5х-4х-8у= -8+2
6х-3у-24у=12-6
х-8у= -6
6х-27у=6
Выразим х через у в первом уравнении, подставим выражение во второе уравнение и вычислим у:
х=8у-6
6(8у-6)-27у=6
48у-36-27у=6
21у=6+36
21у=42
у=2
Теперь вычисленное значение у подставляем в любое их двух уравнений системы и вычисляем х:
х-8у= -6
х-8*2= -6
х-16= -6
х= -6+16
х=10
Решение системы уравнений х=10
у=2
б)2х-3=5(х-у)
2(3х-1)=4у-5
2х-3=5х-5у
6х-2=4у-5
2х-5х+5у=3
6х-4у= -5+2
-3х+5у=3
6х-4у= -3
Умножим первое уравнение на 2, чтобы решить систему методом алгебраического сложения.
После умножения:
-6х+10у=6
6х-4у= -3
Складываем уравнения:
-6х+6х+10у-4у=6-3
6у=3
у=1/2 (или 0,5)
Теперь вычисленное значение у подставляем в любое их двух уравнений системы и вычисляем х:
6х-4у= -3
6х-4*0,5= -3
6х-2= -3
6х= -3+2
6х= -1
х= -1/6
Решение системы уравнений х= -1/6
у=1/2
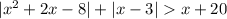
Имеем неравенство, содержащее несколько модулей.
Если неравенство содержит несколько различных модулей, то находят значения 
, при которых выражение, стоящее под знаком модуля, равно нулю. Найденные значения разбивают числовую прямую на интервалы, на каждом из которых выражение под модулем сохраняет знак. А потом на каждом интервале раскрывают модули и решают полученную систему. Объединение решений составляет множество решений данного неравенства.
1) Найдем нули модулей:
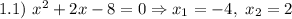
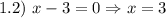
2) Начертим числовую координатную прямую и отметим найденные нули модулей, которые разбивают данную ось на 4 области (см. вложение).
3) Решим систему уравнений на каждом интервале, раскрывая модуль на каждом участке с правила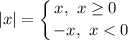 
(при этом где-то нужно ноль модуля включить):
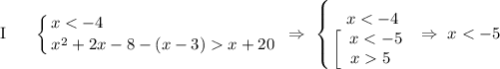
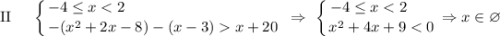
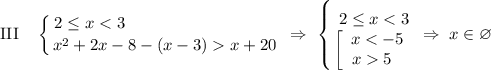
ответ: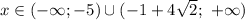 
b1=2. b2=-2 b3= -6. b4= -18
а в общем сам вопрос не совсем понятен, если ты не знаешь как вычислять геометрическую прогрессию, тогда просто вместо буквы n, подставляешь нужное число и решаешь)