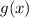;
;
и будет искомой фигурой.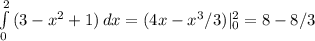
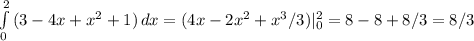
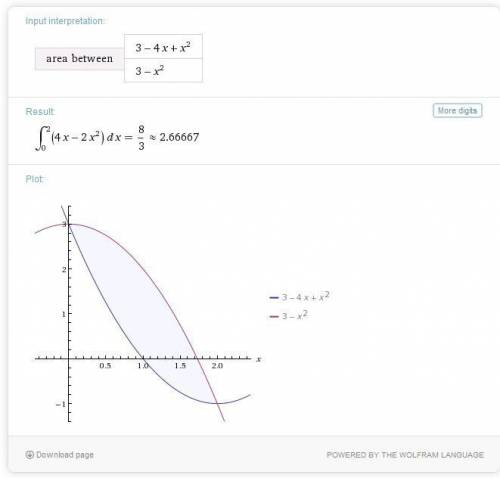
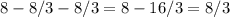(кв. ед.)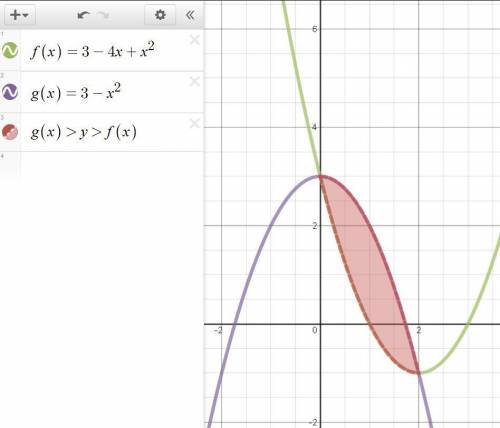
Напишем формулу для суммы 9 членов геометрической прогрессии
s9=(b1*(q^9-1))/(q-1)
Напишем формулу для суммы 18 членов геометрической прогрессии
s18=(b1*(q^18-1))/(q-1)
512=2^9
s9/(s18-s9)=2^9
GПеревернем дробь
(s18-s9)/s9=1/2^9
Числитель разделим на знаменатель почленно.
1-s18/s9=1/2^9 Отдельно упростим дробь s18/s9
s18/s9=(b1*(q18-1)/(q-1))/(b1*(q9-1)/(q-1)
Сократятся b1 и (q-1)
s18/s9=(q18-1)/(q9-1) разность квадратов
s18/s9=((q:9-1)*(q^9+1))/(q9-1) Сократим на (q^9-1)
s18/s9=q^9+1
Возвращаемся к уравнению
1-s18/s9=1/2^9
1-q^9+1=1/2^9
-q^9=1/2^9
q=-1/2
5(x-2)(x+3)<0
(5х-10)(х+3)<0 - вносим 5 за скобку
5x^2+15x-10x-30<0 - раскрываем скобки
5x^2+5x-30<0 -упрощаем
x^2+x-6<0 - ещё упрощаем
x^2+x-6 = 0
D = 1+24=25=5^2
X1= (-1-5)/2=-3
X2=(-1+5)/2 = 2 - Приравниваем к 0 и решаем как квадратное уравнение
строим числовую прямую и отмечаем на ней корни уравнения.
получили числовые промежутки (-бесконечность;-3); (-3;2);(2;+бесконечность).
дальше подставляем число из любого промежутка и смотрим на значение неравенства.
Получаем промежуток (-3;2)
ответ: (-3;2)