Обозначим cлагаемые за Х,У,Z
(X+Y+Z)/3>=1
Согласно неравенству о среднем арифметическом и среднем геометрическом достаточно доказать :
ХУZ>=1
Вернемся к исходным обозначениям
8abc>=(a+b)(b+c)(a+c)
Снова согласно неравенству о среднем арифметическом и среднем геометрическом видим
a+b>=2sqrt(ab) b+c>=2sqrt(сb) (a+c)>=2sqrt(ac)
поэтому можим заменить сомножители справа на произведение
2sqrt(ab)*2sqrt(aс)*2sqrt(сb)=8abc, что и доказывает неравенство.
Равенство достигается только при а=с=b
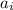- сторона i-ого треугольника
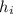- высота i-ого треугольника
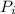- периметр i-ого треугольника
, значит если стороны заданных треугольников образую геометрическую прогрессию, то и их периметры также образуют геометрическую прогрессию.
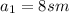. Так как треугольник равносторонний, то все его высоты равны. Найдем длину одной из них. Высота является противолежащим катетом для угла равностороннего треугольника 60 градусов, гипотенузой в таком прямоугольном треугольнике является сторона равностороннего треугольника: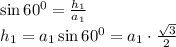
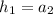, то: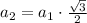
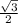(для геометрической прогрессии он и будет являться знаменателем).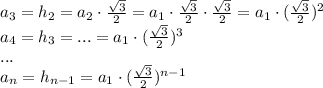
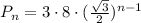
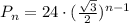- общая формула n-ого члена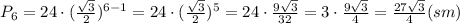
х 1 0 -2
у 5 3 -1
х 1 0 -2
у 7 6 10