Представим через переменные х и у и систему, тогда
х-у=24,
ху=481(система).
из 1 уравнения можно выразить x, и полученное выражения подставить во второе уравнение системы
x=24+y,
(24+y)*y=481. (система)
в полученном втором уравнении раскрываем скобки, переносим числа все в лево, приравниваем к нулю и решаем через дискриминат:
y^2+24y-481=0
D=576+4*1*(-481)=2500 (√2500=50)
y1=(-24+50)/2=13
y2=(-24-50)/2=-74 посторонний корень, т.к. не натуральное чило)
И полученные значения y подставляем в уравнения
x-y=24
x=24+13
x=37
проверяем значения, подставив их во второе уравнение
xy=481
13*37=481 => x=13, y=37
ответ: x=13, y=37
Объяснение:
1. Найдите промежутки возрастания и убывания:
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если "+", функция возрастает, "-" - убывает.
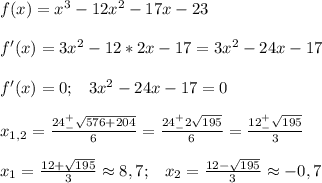
См. рис.
Функция возрастает при х ∈ [-∞; -0,7]∪[8,7; +∞]
или
![\displaystyle x\in [- \infty ;\;\frac{12-\sqrt{195} }{3} ]\cup [\frac{12+\sqrt{195} }{3};\;+ \infty ]](/tpl/images/4664/9108/8e18d.png)
Функция убывает при х ∈ [-0,7; 8,7]
или
![\displaystyle x\in[\frac{12-\sqrt{195} }{3};\;\frac{12+\sqrt{195} }{3} ]](/tpl/images/4664/9108/36d34.png)
2. Найдите стационарные точки:
Точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
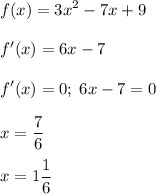
3. Найдите локальные максимумы и минимумы функции.
Найдем производную, приравняем к нулю, найдем корни.
Определим знаки производной на промежутках. Если производная меняет знак с "+" на "-", то будет точка максимума. Если производная меняет знак с "-" на "+" - точка минимума.
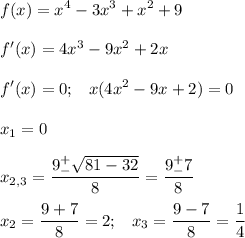
См. рис.
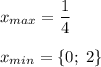

Ели учитывается и все элементы входят в соединение, то это перестановки - первая задача.
Если учитывается и не все элементы входят в выборку, то размещение