№1.
Если трехчлен (2х²- 7х+а) содержит множитель ( х - 4), значит один из корней уравнения 2х²- 7х+а= 0 равен 4, т.е. х=4
Подставим х=4 в уравнение 2х²- 7х+а=0 и найдем а.
2·4²- 7·4+а =0
а=28-32
а= - 4
№2.
4х²+ ах + 6 содержит множитель ( 2х + 1)
1)2х+1=0
х= - 0,5 - это первый корень уравнения 4х²+ах+6=0
2) Делим обе части уравнения 4х²+ах+6=0 на 4 и получим приведенное квадратное уравнение:
х²+0,25ах+1,5=0
3) По теореме Виета для приведенного квадратного уравнения найдем второй корень,
х₁ * х₂ = 1,5
х₂=1,5 : (-0,5)
х₂= - 3
4) По теореме Виета для приведенного квадратного уравнения найдем второй коэффициент, стоящий при х.
х₁+х₂= -0,25а
- 0,25а = - 0,5 + (-3)
- 0,25а = - 3,5
а = - 3,5 : (-0,25)
а = 14
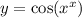
Мы видим, что данная функция является сложной, поэтому будем её дифференцировать как сложную.
Формула
d/dx( f(g(x)) ) = f'(g(x)) × g'(x), где в нашем случае f(x) = cos(x), а g(x) = x^x.
Для применения правила дифференцирования сложной функции, заменим x^x новой переменной t.
Дифференцируем
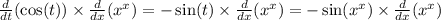
Для упрощения производной запишем х^х как e^( ln(x^x) ).
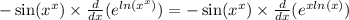
И опять сложная функция.
Дифференцируем её аналогично:
f(x) = e^x, g(x) = xln(x)
Заменим xln(x) перевенной k:
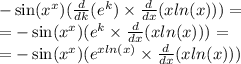
За правилом производной произведения имеем:
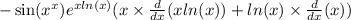
Вычисляем все производные и получаем:
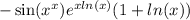
Это и есть ответ.
2t^2+3t-2=0
D=9+16=25
t1=(-3-5)/4=-2 посторонний, т.к. |t|<=0
t2=(-3+5)/4=1/2
вернёмся к замене
sinx=1/2
x=(-1)^n Π/6+Πn, n€Z
или можно записать так:
x1=Π/6+2Πn, n€Z
x2=5Π/6+2Πn, n€Z
2) 8cos^4x-6(1-sin^2x)+1==0
8cos^4x+6cos^2x-5=0
Пусть t=cos^2x, где t€[-1;1]
8t^2+6t-5=0
t1=-5/4 посторонний
t2=1/2
Вернёмся к замене
cos^2x=1/2
cosx=+-√2/2
Распишем отдельно
cosx=√2/2
x=+-arccos√2/2+2Πn, n€Z
x=+-Π/4+2Πn, n€Z
cosx=-√2/2
x=+-arccos(-√2/2)+2Πn, n€Z
x=+-(Π-Π/4)+2Πn, n€Z
x=+-3Π/4+2Πn, n€Z
ответ: +-3Π/4+2Πn, +-Π/4+2Πn, n€Z