№1.
Если трехчлен (2х²- 7х+а) содержит множитель ( х - 4), значит один из корней уравнения 2х²- 7х+а= 0 равен 4, т.е. х=4
Подставим х=4 в уравнение 2х²- 7х+а=0 и найдем а.
2·4²- 7·4+а =0
а=28-32
а= - 4
№2.
4х²+ ах + 6 содержит множитель ( 2х + 1)
1)2х+1=0
х= - 0,5 - это первый корень уравнения 4х²+ах+6=0
2) Делим обе части уравнения 4х²+ах+6=0 на 4 и получим приведенное квадратное уравнение:
х²+0,25ах+1,5=0
3) По теореме Виета для приведенного квадратного уравнения найдем второй корень,
х₁ * х₂ = 1,5
х₂=1,5 : (-0,5)
х₂= - 3
4) По теореме Виета для приведенного квадратного уравнения найдем второй коэффициент, стоящий при х.
х₁+х₂= -0,25а
- 0,25а = - 0,5 + (-3)
- 0,25а = - 3,5
а = - 3,5 : (-0,25)
а = 14
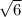/3
Объяснение:
по формуле разности квадратов дух чисел мы знаем что
a^2-b^2=(a-b)*(a+b) У нас здесь корни чтобы избавлятся от корней мы умножаем их только на одну из них например 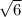+3 а дальше я покажу на листочке и объяснять буду
мы здесь умножали числа и у нас на знаменателе одни и те
же числа толко один + другой - это приведет к формулу разности квадратов и у нас остается 6-9= -3. Теперь в числителе мы раскрываем скобки и у нас получится вот
такое выражение 2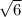+6-6-3 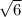6-ки сократятся и остается
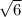-. Вспомните у нас в знаменателе получился -3 а в числителе остался -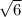. Теперь минусы сократятся и остается 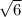/3. ответ: 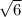/3
x - 1 =< 3x + 2
-3x - 5x > -2 + 1
x - 3x =< 2 + 1
-8x > -1 | : (-1)
-2x =< 3 | : (-1)
8x < 1
2x >= -3
x < 1/8
x >= -1,5
ответ: x принадлежит [-1,5; 1/8)