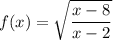
Подкоренное выражение должно быть неотрицательным, а знаменатель не равен нулю. При записи первого условия, второе учитывается. Тогда имеем:
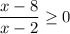
Решим методом интервалов:
Отмечаем на координатной прямой точки, в которых выражения из знаменателя и числителя обращаются в ноль. И выкалываем 2 т.к. на ноль делить нельзя. Мы получили 3 интервала. Перед дробью знак положителен, поэтому на правом интервале ставим "плюс", далее чередуем знак через каждую отмеченную точку (нету чётных степеней, где знак может не измениться). Нас интересует, когда больше или равно, поэтому выбираем интервалы с плюсом, учитывая их границы.
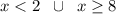
ответ: x∈(-∞;2)∪[8;+∞).

Объяснение:
а) 0,5 х = -2,5
х = -2,5 : 0,5
х = -5
б) 7х - (х + 2) = 10
7х - х - 2 = 10
6х = 10 + 2
6х = 12
х = 12 : 6
х = 2
в) 3х + 2 = 0
3х = -2
х = -2/3
г) 0,7 + 2х = 3х + 1,7
3х -2х =0,7 - 1,7
х = -1
д) В зависимости от пропущенного знака
2х - 5 = х - 32 или 2х +5 = х - 32
2х - х = -32 + 5 2х - х = -32 - 5
х = -27 х = -37
2. Пусть в первом ящике х кг огурцов, тогда во втором ящике х+8 кг огурцов. По условию задачи в двух ящиках 48 кг огурцов. Тогда составим и решим уравнение:
х + х + 8 = 48
2х = 48 - 8
2х = 40
х = 40 : 2
х = 20
Значит, в первом ящике было 20 кг огурцов, тогда во втором ящике было х + 8 = 20 + 8 = 28 кг огурцов.
(x+1)ˇ2.(x-1)ˇ2+(x-7)ˇ2.(x+1)ˇ2=0
(x+1)ˇ2 ( (x-1)ˇ2 + (x-7)ˇ2)=0
a)(x+1)ˇ2 =0, x+1=0, x=-1
b)(x-1)ˇ2+(x-7)ˇ2=0 nelzja icpolnit, dalše rešenie poetomy ne polučajem.
Ect tolko rešeniem x=-1.