Найдите наименьшее положительное значение p+k, если известно: 1+tg p= 2/(1+tg k) варианты ответов √3п/2 ; п/3 ; п с решением

👇

Ответ:

WorkoutEdik

08.03.2022

Область определения:
tg k =/= -1; k =/= -pi/4 + pi*k
Умножаем все на (1+tg k)
(1 + tg p)(1 + tg k) = 2
1 + tg p + tg k + tg p*tg k = 2
tg p + tg k + tg p*tg k = 1
tg p + tg k = 1 - tg p*tg k
По известной формуле тангенса суммы аргументов
tg (p + k) = (tg p + tg k) / (1 - tg p*tg k) = (tg p + tg k) / (tg p + tg k) = 1
p + k = pi/4 + pi*k
Наименьшее положительное значение равно pi/4

4,8(51 оценок)

Открыть все ответы

Ответ:

БиологКоля

08.03.2022

Х- скорость автомобиля 150/х - время за которое проедет автомобиль весь путь х+20 - скорость мотоциклиста 150/(х+20) - время за которое проедет мотоциклист переведём 1ч15м в минуты=1*60+15=75мин составим уравнение: 150/(х+20)-150/х=75 общий знаменатель х(х+20) получим квадратное уравнение: -1,25х^2-25х-3000=0 решаем через дискриминант д=625+4*1,25*3000=15625 х1=(-25-125)/2,5 - не имеет значения, так как скорость не может быть отрицательной х2=(-25+125)/2,5=40км/ч - скорость автомобиля значит скорость мотоциклиста 40+20=60км/ч ответ: скорость автомобиля=40км/ч и скорость мотоциклиста = 60км/ч

4,6(73 оценок)

Ответ:

Lilifvg

08.03.2022

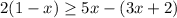
а) $2(1-x) \geq 5x-(3x+2)$
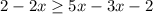
$2-2x \geq 5x-3x-2$
$-4x \geq -4$ $-4x \geq -4$
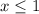
$x \leq 1$

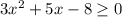
б) $3x^{2}+5x-8 \geq 0$
Вводим функцию: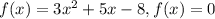
$f(x)=3x^{2}+5x-8, f(x)=0$
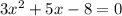
$3x^{2}+5x-8=0$
D=25+96=121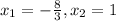
$x_{1}=-\frac{8}{3}, x_{2}=1$
Рисуешь числовую прямую для x, отмечаешь эти две точки по возрастанию, знаки справа налево: +-+. А тебе нужно 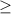$\geq$ , значит ответом два промежутка:
$(-\infty; -\frac{8}{3}] \cup [1;+\infty]$

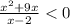
в) $\frac{x^{2}+9x}{x-2} < 0$
Так же как и в примере б вводишь функцию для всей дроби, приравниваешь к нулю. Но так как в этом примере в знаменателе есть х, приравнивание будет выглядить так: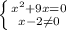
$\left \{ {{x^{2}+9x=0} \atop {x-2 \neq 0}} \right.$

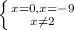
$\left \{ {{x=0, x=-9} \atop {x \neq 2}} \right.$
Отмечаешь три точки на числовой прямой в порядке возрастания. Знаки расставляешь справа налево: +-+-
Потому что перед иксом с большей степенью стоит +
Тебе подойдут промежутки: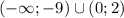
$(- \infty; -9) \cup (0;2)$
Незакрашенные потому что у тебя в условии строго <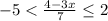

$-5 < \frac{4-3x}{7} \leq 2$
В двойных неравенствах к иксу подбираются постепенно, избавляясь от чисел в середине. Нужно помнить о том, что при делении или умножении на минус знаки неравенства меняются.
Сначала умножим на 7(чтобы в центре сократилась семерка), знак не меняем, потому что 7 - положительна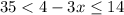
$35 < 4-3x \leq 14$
Теперь избавимся от 4, отнимая ее от всех частей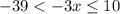
$-39 < -3x \leq 10$
Делим на -3 и МЕНЯЕМ ЗНАК, так как 3 отрицательно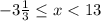
$-3\frac{1}{3} \leq x<13$

Чтобы найти в последнем обл. опр., необходимо найти решения неравенства 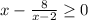$x-\frac{8}{x-2} \geq 0$
Так как подкоренное выражение должно быть больше или ровно 0.
Это уже как-нибудь самостоятельно, глядя на предыдущие примеры
Успехов :)