
 => n=50 шт.
=> n=50 шт.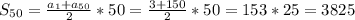 - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 3.
- это сумма всех натуральных чисел, не превосходящих 150, делящихся на 3.
 => k=37 шт.
=> k=37 шт.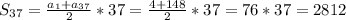 - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 4.
- это сумма всех натуральных чисел, не превосходящих 150, делящихся на 4.
 => n=50 шт.
=> n=50 шт.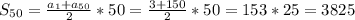 - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 3.
- это сумма всех натуральных чисел, не превосходящих 150, делящихся на 3.
 => k=37 шт.
=> k=37 шт.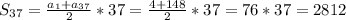 - это сумма всех натуральных чисел, не превосходящих 150, делящихся на 4.
- это сумма всех натуральных чисел, не превосходящих 150, делящихся на 4.
(x-4-5x)(x-4+5x)=(-4x-4)(6x-4)=-4(x+1)*2(3x-2)=8(x+1)(2-3x)
2
(a-b)(a+b)-4(b+a)=(a+b)(a-b-4)