Объяснение:
у=х-4 х€[-1; 7]
k=1>0 ===> y(x) - возрастающая
функция.
а1.
Наименьшее значение функция
принимает в левой крайней точ
ке заданного отрезка х=-1 :
у(-1)=-1-4=-5
а2.
Наибольшее значение функция
принимает в правой крайне точ
ке заданного отрезка х=7 :
у(7)=7-4=3
б1.
Если у=0, то:
0=х-4
-х=-4
х=4
Значение у=0 функция достига
ет в точке сабсциссой, равной 4.
б2.
х-4<0
х<4
Вывод:
функция принимает отрицтаель
ные значения у<0 при
х€(-оо; 4).
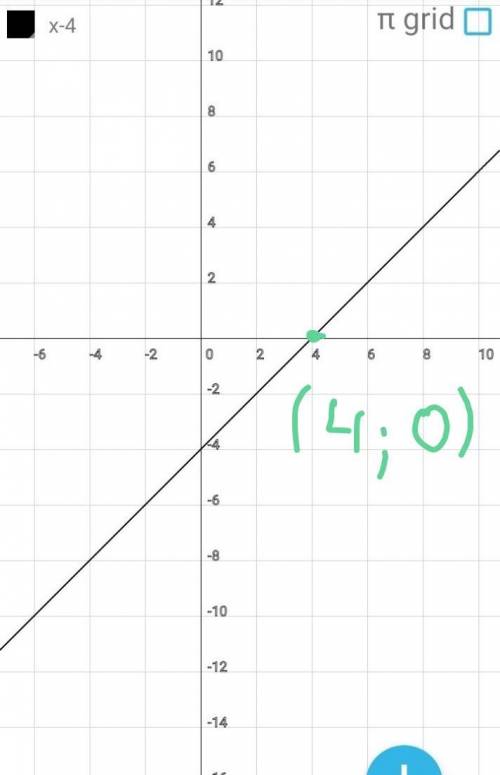
Строим график функции
у=х-4
Составим и заполним таб
личку: достаточно двух точек,
так как графиком линейной
функции является прямая ли
ния.
х -1 3
у -5 -1

Объяснение:
у=х-4 х€[-1; 7]
k=1>0 ===> y(x) - возрастающая
функция.
а1.
Наименьшее значение функция
принимает в левой крайней точ
ке заданного отрезка х=-1 :
у(-1)=-1-4=-5
а2.
Наибольшее значение функция
принимает в правой крайне точ
ке заданного отрезка х=7 :
у(7)=7-4=3
б1.
Если у=0, то:
0=х-4
-х=-4
х=4
Значение у=0 функция достига
ет в точке сабсциссой, равной 4.
б2.
х-4<0
х<4
Вывод:
функция принимает отрицтаель
ные значения у<0 при
х€(-оо; 4).
Строим график функции
у=х-4
Составим и заполним таб
личку: достаточно двух точек,
так как графиком линейной
функции является прямая ли
ния.
х -1 3
у -5 -1



2)
а) 8х^2-8у^2=8(x-y)(x+y)
б)-а^2+6а-9=-(x-3)^2
в)аb^3-ba^3=ab(b-a)(b+a)
3)
а) 12x3-27xy2=3x(2x-3y)(2x+3y)
б) a(x-y)-b(x-y)=(a-b)(x-y)
в) (a-3)2-4(a-3)=(a-3)(a-7)
г) -4x4+20x2 =-4x^2(x^2-5)
д) 2(x-y) - (y -х} = 3(x-y)
4)
а) (x^2-1) (x^2+3) = (x^2+1)^2+x
x^4-x^2+3x^2-3=x^4+2x^2+1+x
x=-4
б) (x^2-6) (x^2+2) = (x^2-2)^2-x
x^4-6x^2+2x^2-12=x^4-4x^2+4-x
x=16