Пусть вкладчик положил рублей в банк. Через год вкладчик получит рублей. После того, как снял деньги, у него остается рублей. Известно, что на счёте осталась сумма, равная половине первоначального вклада. Составим уравнение
В конце второго года хранения вкладчик получит рублей. Подставив значение х, получим рублей.
ответ: на счету у вкладчика в конце второго года хранения будет 745 рублей.
Вопрос "как решать систему уравнений" не совсем уместен. Существует множество различных приёмов решения систем. Но на вопрос ответить можно. Есть два основных решения систем: 1)Подстановкой 2)Сложением В зависимости от ситуации используется первый или второй
В нашей системе выгоднее решать именно подстановкой. Смотрите, у нас же в первом уравнении уже выражен y. А во втором уравнении фигурирует тот же самый y. Мы же знаем, чему он равен, из первого уравнения. Так что подставим во второе уравнение вместо y x + 1.
Получили обыкновенное уравнение с одной переменной, которое и решаем. Обычное квадратное уравнение. Решаем его(можно через дискриминант, а можно по теореме Виета) Мы получили иксы. Но это ещё не всё. Ведь решить систему уравнений - значит найти не только иксы, но и соответствующие им игреки. Так что для каждого икса найдём ему пару - соответствующий y. А откуда найдём? Из первого уравнения(теперь икс у нас есть, можем найти y)
1)x = 3, тогда y = x + 1 = 3 + 1 = 4 2)x = -2, тогда y = x + 1 = -2 + 1 = -1 Для КАЖДОГО x мы нашил свой y, поэтому можем говорить о том, что система решена. Записываем ответ. В ответе пишем все найденные пары, сначала x, потом y. ответ: (3, 4); (-2, -1)
Пусть вкладчик положил
рублей в банк. Через год вкладчик получит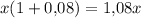 
рублей. После того, как снял деньги, у него остается 
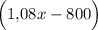рублей. Известно, что на счёте осталась сумма, равная половине первоначального вклада. Составим уравнение
В конце второго года хранения вкладчик получит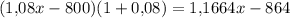
рублей. Подставив значение х, получим 
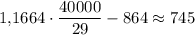рублей.
ответ: на счету у вкладчика в конце второго года хранения будет 745 рублей.