Пусть скорость автомобиля равна х км/ч. Скорость после увеличения равна (x+10) км/ч. Автомобиль за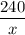 
ч из пункта А в пункт В. За первую половину пути из пункта В в пункт А он проехал 
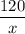часов, а оставшееся вреся - 
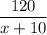часов. Зная, что на обратный путь автомобиль затратил 25 ч меньше, чем на путь от А в В, составим и решим уравнение:
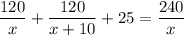
Домножим левую и правую части уравнения на x(x+10)/5
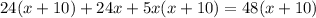
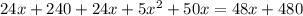
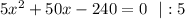
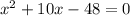
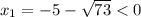— посторонний корень
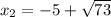
Однако в условии, что-то не так. Расстояние 240 км можно преодолеть намного меньше чем 25 часов.. Не такое уж и большое расстояние
Объяснение:
1) x²+16x-14y+y²+113=0
x²+16x+y²-14y=-113
Допустим:
x²+16x=-57
x²+16x+57=0; D=256-228=28
x₁=(-16-√28)/2=(-16-2√7)/2=-8-√7
x₂=(-16+√28)/2=√7 -8
y²-14y=-56
y²-14y+56=0; D=196-224=-28 - при D<0 уравнение не имеет решений.
Следовательно, x и y не имеют значений при x²+16x-14y+y²+113=0.
2) x²-10x+6y+y²+34=0
x²-10x+y²+6y=-34
Допустим:
x²-10x=-17
x²-10x+17=0; D=100-68=32
x₁=(10-√32)/2=(10-4√2)/2=5-2√2
x₂=(10+√32)/2=5+2√2
y²+6y=-17
y²+6y+17=0; D=36-68=-32 - при D<0 уравнение не имеет решений.
Следовательно, x и y не имеют значений при x²-10x+6y+y²+34=0.
2) ( b + 4)^3 + 4^3 = (b + 4 + 4)(b^2+8b+16 -4b-16+16) =(b + 8)(b^2+4b+16)
3) ( x^2 + 1)^2 - 4x^2 = ( x^2 + 1 - 2x)(x^2 + 1 + 2x)=(x^2-2x+1)(x^2+2x+1)=
= (x - 1)(x- 1)(x+ 1)(x+ 1)
4) (y^2 + 2y)^2 - 1 = (y^2 + 2y - 1)(y^2 + 2y + 1) = (y + 2y - 1)(y + 1)(y + 1)
5) ( 9 - c^2 - 6c)(9 + c^2 + 6c)=( - c^2 - 6c + 9)(c^2 + 6c + 9)
6) (4m - m+ n)(4m + m - n)= (3m + n)(5m - n)