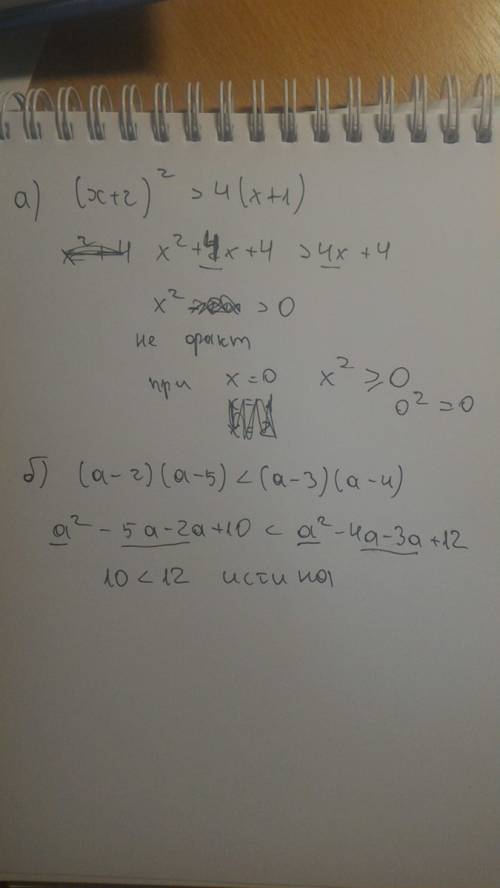
по примеру реши.
x^3 - 6x^2 + 11x - 6 = 0 можно, конечно, решить формулой кардано для решения кубических уравнений, но это долго и трудно. проще подобрать корни схемой горнера. возможные рациональные корни x = a/b, где а - делитель свободного члена, b - делитель старшего коэффициента. x = 1, -1, 2, -2, 3, -3, 6, -6 находишь значения в этих точках. y(1) = 1 - 6 + 11 - 6 = 0 - повезло сразу! теперь раскладываем: x^3 - x^2 - 5x^2 + 5x + 6x - 6 = 0 (x - 1)(x^2 - 5x + 6) = 0 (x - 1)(x - 2)(x - 3) = 0 ответ: x1 = 1, x2 = 2, x3 = 3
ответ: 5/12
Объяснение:Количество всевозможных подбрасывания двух игральных костей равно 6*6 = 36 из них благоприятствуют те, у которых на первой игральной кости число очков больше, чем на второй:
1) Если на первой игральной кости выпало 1, то на второй: {2;3;4;5;6} - 5 вариантов
Если выпало 2 очка, то на второй кости: {3;4;5;6} - 4 варианта
Если выпало 3 очка, то на второй кости: {4;5;6} - 3 варианта
Если выпало 4 очка, то на второй кости: {5;6} - 2 варианта
Если выпало 5 очков, то на второй кости: {6} - 1 вариант
Всего вариантов: 5+4+3+2+1=15
P = m/n
где m - число благоприятных исходов; n - число всевозможных исходов
m = 15;
n = 36
P = 15/36 = 5/12