D(y)=(-беск;0) (0;+беск)
y'=(4x^-1)'+(x^-4)'=-4x^-2 -4x^-5=-4/x^2-4/x^5=(-4x^3-4)/x^5=-4((x^3+1))/x^5
y'=0 x^3+1=0 x^3=-1 x=-1 х не равен 0
чертим луч -1 0
знак производной - + -
поведение функции убыв возр убывает
х=-1 точка минимума f(-1)=-4+1=-3
x=0 вертикальная асимптота
поведение функции в бесконечности lim(4/x+1/x^4)=0+0=0
lim(хстремится к 0) (4x^3+1)/x^4=беск
f(-x)=4/(-x)+1/(-x)^4=-4/x+1/x^4 функция не является ни четной ни нечетной
чтобы найти точки , надо найти вторую производную, решить y''=0 там же определяется выпуклость(y''<0) вогнутость(y''>0)
Для точности построения -таблица
x -3 -2 -1 -0,1 0,1 2
у -1,3 -1,9 -3 2,1
f(-0,1)=-40+1/0,0001=-40+10000=9960
f(0,1)=40+10000=10040 Стройте график. Не забудьте, что прямая х=0 графикоь не пере секается
нули функции у=0 ( 4x^3+1)/x^4=0 x^3=-1/4 x=корень 3-ьей степени из(-0,25)
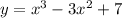
1. Функция многочлен, а значит область определения функции вся вещественная ось.
2. Многочлены будут четными, если содержат только четные степени переменной и наоборот нечетными при нечетных степенях. в нашем случае функция является ни четноой, ни нечетной. Функция непериодическая.
3. Функция не имеет асимптот.
4. Поскольку функция имеет степень 3, то ее график не имеет ни горизонтальных, ни наклонных асимптот.
5. найдем пересечение с осью Оу для этого найдем значене у при х=0
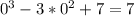
и пересечение с осью Ох для этого решим уравнение 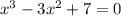
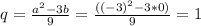
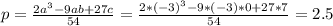
получаем каноническое уравнение
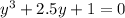
найдем Q
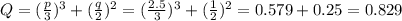
так как Q>0, то по методу Кардано уравнение имеет один действительный корень
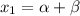
![\alpha=\sqrt[3]{-\frac{q}{2}+\sqrt{Q}}=\sqrt[3]{-\frac{1}{2}+\sqrt{0.829}}](/tpl/images/0172/1280/2c7f2.png)
![\beta=\sqrt[3]{-\frac{q}{2}-\sqrt{Q}}=\sqrt[3]{-\frac{1}{2}-\sqrt{0.829}}](/tpl/images/0172/1280/5f9bf.png)
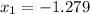
6. производная функции будет 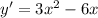
найдем интервалы возрастания и убывания
решим неравенство 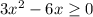
решим квадртное уравнение
дискриминант будет равен 36
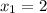
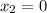
следовательно на интервалах ]-∞;0] и [2;+∞[ функция возрастает, а между ними функция убывает
и в итоге строим график

-12х+17у=-87
х=-у
второе уравнение умножим на 12 и сложим с первым
-12х+17у=-87
+
12х=-12у
-12х+17у+12х=-87-12у
17у=-87-12у
17у+12у=-87
29у=-87
у=-87/29=-3
x=-y=-(-3)=3
ответ (3,-3)
проверка
-12*3+17*(-3)=-36-51=-87 (верно)