
пусть хкм/ч-собственная скорость лодки,тогда 10/(х+3) ч-время по течению,а 15/(х-3) ч-время против течения.
Составим уравнение:
10 + 15 = 10 - приведем к общему знаменателю- 3(х-3)(х+3)
х+3 х-3 3
10(3х-9)+15(3х+9)=10(х²-9)
30х-90+45х+135=10х²-90
75х+135-10х²=0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=75²-4*(-10)*135=5625-4*(-10)*135=5625-(-4*10)*135=5625-(-40)*135=5625-(-40*135)=5625-(-5400)=5625+5400=√11025=105
Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(105-75)/(2*(-10))=30/(2*(-10))=30/(-2*10)=30/(-20)=-30/20=-(3//2)=-1.5;
x₂=(-105-75)/(2*(-10))=-180/(2*(-10))=-180/(-2*10)=-180/(-20)=-(-180/20)=-(-9)=9.
Отрицательной скорость не может быть,значит х=9км/ч
ответ:9км/ч-собственная скорость моторной лодки.
а) 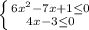
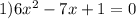
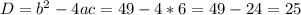
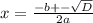
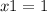
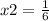
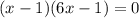
Строим координатную прямую и отмечаем на ней закрашенными точками 1\6 и 1
Получается, что х принадлежит [1\6;1]
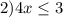
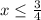
Снова строим координатную прямую и отмечаем на неё закрашенную точку 3\4. Получаем, что х принадлежит ![(-\infty;\frac{3}{4}]](/tpl/images/0077/2198/d1207.png)
3) Общий
Отмечаем на координатной прямой все точки 1\6, 3\4 и 1.
Совмещаем графики и получаем решение системы уравнений.
x принадлежит [1\6;\3\4]
Напоминаю, что вид скобок имеет значение.
б) 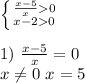
Строим координатную прямую и отмечаем на ней выколотые точки 0 и 5. х принадлежит 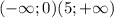
2) х>2
Строем координатную прямую с выколотой точкой 2 и получаем, что х принадлежит 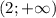
Объединяем значения на координатной прямой и получаем решение системы уравнений. х принадлежит 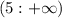
у - 2-е число
2х + 3у = 23 |*3 6x + 9y = 69
4у - 3х = 8 |*2 -6x + 8y = 16
+
17y = 85
y = 5
2х + 3у = 23; 2x = 23 - 15; 2x = 8; x=4.
Проверка: 8+15 = 23; 23=23
Составляешь уравнения по условию. Методом сложения их решаешь (первое умножаешь на 3, второе на 2. 6х = - 6х сокращаешь, а далее элементарно решаешь)