Область определения функции. ОДЗ: -00<x<+00
Точка пересечения графика функции с осью координат Y:График пересекает ось Y, когда x равняется 0: подставляем x=0 в x^2+4*x+3.
а) Выбрать 4 ромашки можно 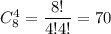 а 3 незабудки -
а 3 незабудки - 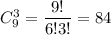 По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно
По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно 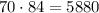
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно 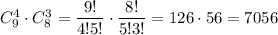 Выбрать пять незабудки и две ромашки можно
Выбрать пять незабудки и две ромашки можно 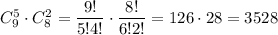 Выбрать шесть цветов незабудки и одна ромашку можно
Выбрать шесть цветов незабудки и одна ромашку можно 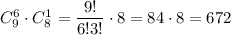 И наконец выбрать семь цветов незабудки можно
И наконец выбрать семь цветов незабудки можно 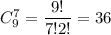 По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
==========
а) Необходимо найти зависимость площади фигуры, содержащей точку
Прежде всего, покажем, что следует рассмотреть несколько случаев получаемых при отсечении от квадрата прямой фигур: может получиться как треугольник (смотрите рисунок 2), так и трапеция (смотрите рисунок 3).
Рассмотрим оба случая отдельно.
СЛУЧАЙ 1 (треугольник)
Имеем треугольник
При любом значении
Теперь подумаем, как от величины
Мы нашли зависимость катета
Напомню формулу площади:
Где
Отлично, зависимость найдена. Но это только при
СЛУЧАЙ 2 (трапеция)
Как мы уже отметили, при
Сразу отметим какие стороны трапеции зависят от
Отсюда:
Остается найти
Вспоминаем где нам нужно было
Теперь же найдем площадь трапеции:
======
Итак, мы решили только первую часть задания. Что же выходит? Площадь фигуры, содержащей вершину