Объяснение:
1) log₂(x-1)=1
используем определение логарифма -
логарифмом числа b по основанию a ( logₐb ) называется такое число n, что b=aⁿ, у нас а =2, b = (x-1), n = 1 подставим наши значения
(х-1)=2¹ ⇒ х-1=2⇒х=3 отрезок (0;3]
2) log₂(x-1)≤0
по определению логарифма b >0, у нас х-1 > 0 ⇒ х > 1 это первое условие
ищем второе. сначала решаем уравнение log₂(x-1)=0
используем свойство логарифма logₐ1=0 имеем х-1 = 1 ⇒ х=2
на отрезке (1;2] проверим знак логарифма
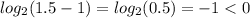
это наш отрезок (1;2]
3)
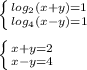
x=3; y=-1
4)
log₂(4-x)≤1
4-x>1 ⇒ x < 4
log₂(4-x)=1 ⇒ 2=4-x ⇒x=2
[2;4)
5)
log₇log₂log₇49
раскручиваем справа
log₇log₂log₇49=log₇log₂2=log₇1=0
log₁₂3+log₁₂4= log₁₂3*4=log₁₂12=1
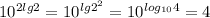
Тригонометрия – математическая дисциплина, изучающая зависимость между сторонами и углами треугольника, является разделом геометрии, тригонометрические функции являются объектом изучения математического анализа, а тригонометрические уравнения изучаются методами алгебры.
Тригонометрические функции возникли в Древней Греции в связи с исследованиями в астрономии и геометрии. Отношения сторон в прямоугольном треугольнике, которые по существу и являются тригонометрическими функциями, встречаются уже в Ш в. до н. э. в работах Евклида, Архимеда, Аполлония Пергского и др. Тригонометрия от греческих: trigonom – “треугольник”, metreo – “измеряю”, изучает зависимость между сторонами и углами треугольника.
Тригонометрия возникла из пратических нужд человека. С ее можно определить расстояния до недоступных предметов. Она существенно упрощает процесс геодезической съемки местности, нужный для составления карт.
Зачатки тригонометрических познаний родились в древности. Жрецы постоянно наблюдали за небом, за перемещением звезд. На раннем этапе тригонометрия развивалась в тесной связи с астрономией и являлась ее вс разделом.
Исторически теоремы синусов сферической геометрии предшествовали теоремам плоской геометрии. Потребность людей в знаниях по астрономии, необходимых для исчисления времени, возникла прежде других потребностей человека, связанных с измерением углов. Исходя из геоцентрической гипетезы Вселенной, древнегреческие астрономы рассматривали Землю как шар, находящийся в центре небесной сферы, которая рвномерно вращается вокруг своей оси. При изучении закономерностей движения светил возникли многочисленные математические задачи, связанные со свойствами сферы и фигур, которые образуют на ней большие окружности.
2) a) a^3(3a^5 -14a^3 -1)/a^3 +3a^5 =3a^5 -14a^3 -1 +3a^5 =6a^5 -14a^3 -1
b) 8m^3 +2197n^6 =2^3m^3 +13^3n^6 =(2m +13n²)(4m² -2m*13n² +169n^4) =(2m+13n²)(4m² -26mn² +169n^4)
3) 2.49*1.63 -2.12*1.63 +1.63*0.63 =1.63(2.49 -2,12 +0.63) =1.63*1 =1.63
4) =(4c²y^6 *16c^5y) /16c^4y² =(4c²y^6 *c)/y =4c^3y^5