1). 7x² - 8x²y - 3yz + *
Известная часть многочлена: 7x² - 8х²y - 3yz
Если из данной части вывести переменную х, добавив вместо звездочки, скажем, -(7x² - 8х²y), то останется выражение -3yz, не являющееся многочленом по определению.
Поэтому добавим к оставшемуся выражению -3yz еще у²:
7x² - 8x²y - 3yz + * = -3уz + у²
* = -3yz + y² - 7x² + 8x²y + 3yz
* = y² - 7x² + 8x²y
Вместо у² можно взять любой другой одночлен, не содержащий переменную х.
2). (3n + 8) - (6 - 2n) = 3n + 8 - 6 + 2n = 5n + 2
При любом n ∈ N, выражение 5n + 2 при делении на 5 даст остаток 2.
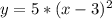
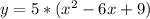
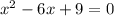
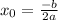
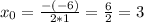
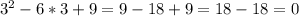
a(4-b)=-3-b2
a=(-3-b2)/(4-b)