x₁ = 2 + 
, y₁ = 2 - 3;
x₂ = 2 -, y₂ = - 3 - 2:
Объяснение:
{ху - х = 4
{2х - у = 7
Выразим y и подставим во второе уравнение
{xy - x = 4
{-y = 7 - 2x
Уберём минус перед y, помножив выражение на (-1)
{xy - x = 4
{y = 2x - 7
Подставляем полученное выражение вместо y
x * (2x - 7) - x = 4
2x² - 7x - x =4
2x² - 8x - 4 = 0
Получаем квадратное уравнение. Сокращаем коэффиценты, деля обе стороны на 2
x² - 4x - 2 = 0
У нас a = 0. По теореме Виета: x₁ + x₂ = −b; x₁ * x₂ = c;
Но для начала проверим дискриминант
D = b² - 4ac
D = 16 - 4 * 1 * (-2)
D = 16 + 8 = 24
Нет такого натурального числа, которое было бы квадратным корнем из 24, поэтому мы не сможем решить теоремой Виета, и продолжаем решать дискриминантом
x₁,₂ = 
x₁ = 
= 
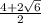= 2 +
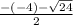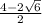x₂ = 
= 
= 2 -
Находим y, подставляя x
2 * (2 + ) - y₁ = 7
4 + 2 - y₁ = 7
- y₁ = 3 - 2
Убираем минус
y₁ = 2 - 3
Ищем y₂
2 * (2 - ) - y₂ = 7
4 - 2 - y₂ = 7
- y₂ = 3 + 2
Снова убираем минус
y₂ = - 3 - 2
ответ: x₁ = 2 + , y₁ = 2 - 3; x₂ = 2 -, y₂ = - 3 - 2;
Нужно использовать следующие свойства числовых неравенств:
1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:
если а < b и с - любое число, то a + c < b + c.
2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:
если а < b и с > 0, то ac < bc;
если а < b и с < 0, то ac >bc.
Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),
а затем и 2,5а - 7 < 2,5b - 7.
ответ: 2,5а - 7 < 2,5b - 7.
(x-1)⁶>0, (x+1)²>0 произведение двух положительных множителей положительно, => и (x-9)⁷>0
метод интервалов:
1. (x-9)⁷=0 или (x-1)⁶=0 или (x+1)²=0
x₁=9, x₂=1, x₃=-1
- + - +
2. [-1][1][9]>x
3. x∈[-1;1]∪[9;∞)