Найдите корни уравнения:
1) 7+2x²=2(x+1)(x+3)
постепенно раскрываем скобки
7+2х²=2(х²+3х+х+3)
7+2х²=2(х²+(3х+х)+3)
7+2х²=2(х²+4х+3)
7+2х²=2х²+8х+6
перенесём всё в правую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
2х²+8х+6-7-2х²=0
группируем или приводим подобные члены
(2х²-2х²)+8х+(6-7)=0
8х-1=0
8х=1
х=1:8
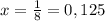
____________________________________________________
7+2·(0,125)²=2(0,125+1)(0,125+3) (это проверка)
7,03125=2·1,125·3,125
7,03125=7,03125
2) (y+4)(y+1)=y-(y-2)(2-y)
постепенно раскрываем скобки
у²+у+4у+4=y-(2y-y²-4+2y)
у²+у+4у+4=y-(-y²+(2y+2y)-4)
у²+у+4у+4=y-(-y²+4y-4)
у²+у+4у+4=y+y²-4y+4
перенесём всё в левую часть и приравняем уравнение к нулю, при этом не забываем сменить знаки на противоположные
у²+у+4у+4-y-y²+4y-4=0
группируем или приводим подобные члены
(у²-y²)+(у+4у-y+4y)+(4-4)=0
8у=0
у=0
(0+4)(0+1)=0-(0-2)(2-0)
4·1=0-(-2·2)
4=0-(-4)
4=0+4
4=4
2) Задача
Обозначим кроликов "к", а фазанов "ф"
у кроликов по 4 лапы, а у фазанов 2
согласно данным условия задачи составляем систему уравнениий:
4к+2ф=100 (1)
к+ф=36 (2)
к=36-ф
4(36-ф)+2ф=100
144-4ф+2ф=100
144-2ф=100
2ф=144-100
2ф=44
ф=44:2
ф=22 (шт.) - фазаны.
к=36-ф=36-22=14 (шт.) - кролики.
ответ: В клетке находятся 14 кроликов и 22 фазана.
1)(3x^2-12)/(1-11x)>0
3(x^2-4)/(11(1/11-x))>0
3(x-2)(x+2)/(11(1/11-x))>0
+ - + -
(-2)(1/11)(2)
(-бескон.;-2)объединено(1/11;2)
2)243*(1/81)^{3x-2}=27^{x+3}
3^{5} *(3^(-4})^{3x-2}=(3^3)^{x+3}
3^{5} *3^{-12x+8}=3^{3x+9}
3^{5-12x+8}=3^{3x+9}
3^{13-12x}=3^{3x+9}
13-12x=3x+9
-12x-3x=9-13
-15x=-4
x=4/15
3)я не уверен, что ты правильно написал функцию проверь.
Мне кажется, что f(x)=1+8x-x^2, а не как у тебя 1+8-x^2
Решу для f(x)=1+8x-x^2
f`(x)=8-2x=2(4-x)
f`(x)=0 при 2(4-x)=0
4-x=0
х=4 принадлежит [2;5)
f(2)=1+8*2-2^2=1+16-4=13
f(4)=1+8*4-4^2=1+32-16=17-наибольшее значение
f(5)=1+8*5-5^2=1+40-25=16
4)2cos(x/2)+sqrt{2}=0
cos(x/2)=-sqrt{2}/2
x/2=pi- pi/4+2pi*n
x/2=3pi/4 +2pi*n |*2
x=6pi/4+4pi*n
x=3pi/2+4pi*n, n принадлежит Z
5)16^{x} -5*4^{x}=-4
(4^{x})^{2} -5*4^{x}+4=0 |t=4^{x}
t^2-5t+4=0
t1=1; t2=4
4^{x}=1 4^{x}=4^{1}
4^{x}=4^{0} x=1
x=0
ответ: 0;1
6) log_{\frac{1}{4}}\frac{3x+2}{2x-7}=-1
(3x+2)/(2x-7)=4
3x+2=4(2x-7)
3x+2=8x-28
3x-8x=-2-28
-5x=-30
x=6
Находим ОДЗ: (3х+2)/(2х-7)>0
3(x+2/3)/(2(x-3,5))>0
+ - +
(-2/3)(3,5)
(-бескон., -2/3) объединено(3,5;+бесконечность)
х=6 входит в область определения
ответ: 6
7)27^{x}<9^{x^2-1}
3^{3x}<3^{2x^2-2}
3x<2x^2 -2
2x^2 -3x-2>0
D=25
x1=2, x2=-1/2
8){x-y=7
{log-2(2x+y)=3
{x-y=7
{2x+y=8
y=8-2x
x-(8-2x)=7
x-8+2x=7
3x=15
x=5
y=8-2*5=-2
ответ:(5;2)
Подробнее - на -
Объяснение:
247/16-х время против течения
247/16+х время по течению, оно на 6ч меньше, чем время против течения.
Составляем уравнение и решаем его
247/16-х - (247/16+х)=6 приводим к общему знаменателю(16+х)(16-х), получаем
247(16+х ) - 247(16-х) = 6(16+х)(16-х)=6(256-х²)
247(16+х-16+х)=1536-6х²
247*2х=1536-6х²
делим на 2
247х=768-3х²
3х²+247х-768=0
Находим корни квадратного уравнения , получаем
Х₁=( -247- √ 2472+4*3*768):2*3= (-247-265):6= отриц.число, скорость течения не может быть отриц. По модулю
Х₂=( -247+ √ 2472+4*3*768):2*3= (-247+265):6=18:6=3 км/ч