Question

1)функция задана формулой y=-2x+3. определите: а) значение функции если значение аргумента равно 3 б) значение аргумента при котором значение функции равно 5 в) проходит ли график функции через точку b (-1; 5) 2)постойте график функции y=5x-4.пользуясь графиком найдите: а) значение функции если значение аргумента равно 1 б) значение аргумента при котором значение функции равно 6. 3) не выполняя построения найдите координаты точек пересечения графика функции y=0.2x-10 с осями координат. 4) при каком значении k график функции y=kx-15 проходит через точку c (-2; -3)? ! !

Answer 1

1. а) значение аргумента равно 3, тогда значение функции:

$\tt y=-2\cdot 3+3=-6+3=-3$

б) Согласно условию значение функции равно 5, то есть,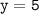 $\tt y=5$, то значение аргумента найдем, решив следующее уравнение:

$\tt 5=-2x+3\\ -2x=2\\ x=-1$

в) Подставляя координаты точки В в график уравнения, получим

$\tt 5=-2\cdot(-1)+3\\ 5=5$

Раз выполняется тождество, следовательно, график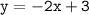 $\tt y=-2x+3$ проходит через точку В(-1;5).

2. Графиком линейной функции является прямая. Для построения прямой достаточно взять две точки, например: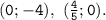 $\tt (0;-4),~(\frac{4}{5} ;0).$

а) значению аргумента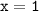 $\tt x=1$ соответствует значение функции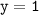 $\tt y=1$

б) значению функции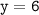 $\tt y=6$ соответствует значение аргумента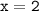 $\tt x=2$

3. Точки пересечения с осью координат Х. График функции пересекает ось Х при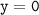 $\tt y=0$, значит нужно решить уравнение:

$\tt 0.2x-10=0\\ x=50$

$\tt (50;0)$ - точка пересечения графика с осью ОХ.

Точки пересечения с осью координат У. График пересекает ось У, когда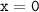 $\tt x=0$, то есть, подставляя х=0 в график уравнения, получим

$\tt y=0.2\cdot 0-10=-10$

$\tt(0;-10)$ - точка пересечения графика с ось ОY.

4. Раз график функции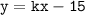 $\tt y=kx-15$ проходит через точку 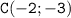$\tt C(-2;-3)$, значит значение 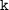$\tt k$ найдем, подставив координаты точки C, имеем

$\tt -3=k\cdot(-2)-15\\ -2k=12\\ k=-6$