Составьте формулу для решения : из пункта м в пункт n со скоростью x км/ч выехал автомобиль. спустя t ч навстречу автомобилю из n со скоростью y км/ч выехал мотоциклист. мотоциклист встретил автомобиль на расстоянии d км от n. найдите расстояние между пунктами m и n. если можно, с подробным решением, распишите, как вы это сделали. на не поскуплюсь, заранее

👇

Ответ:

maks695

20.10.2021

До момента начала движения мотоциклиста автомобиль проехал
x*t км,
по формуле: V=S/t, где V - скорость, S - путь, t - время,
следовательно S=V*t, по условию задачи это x*t
мотоциклисту потребовалось времени до встречи t мот= d/y,
где по условию задачи d - путь мотоциклиста до встречи, а у - скорость
смотри формулу V=S/t => t+S/V
Общее расстояние между пунктами M и N складывается из трех частей:
путь автомобиля до момента движения мотоциклиста, он нам известен x*t
путь мотоциклиста до встречи, по условию это d
путь автомобиля от момента движения мотоциклиста до встречи с ним, он нам не известен, но может быть вычислен по формуле s=V*T,
где V это скорость автомобиля, по условию - x
T - это время движения автомобиля до встречи, оно равно времени движения мотоциклиста. Мы его вычислили t мот=d/y,
т.о. неизвестный отрезок пути равен s=x*d/y
общее расстояние между пунктами равно
S(MN)=x*t+x*d/y+d

4,4(9 оценок)

Открыть все ответы

Ответ:

Лиопольд

20.10.2021

Необходимо было решить 2 первые задачи из документа, но я решил ещё и параметр, который мне понравился.

12. Необходимо решить уравнение

$\displaystyle sin \ 2x = \sqrt{2} \cdot cos\bigg(\frac{7\pi}{2}-x\bigg)$

Формула двойного угла 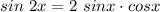$sin \ 2x = 2 \ sinx \cdot cosx$

А также 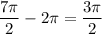$\displaystyle \frac{7\pi}{2}-2\pi=\frac{3\pi}{2}$ , как известно, добавление или вычитание целого периода из аргумента тригонометрической функции ничего не меняет.

Так как в выражении в скобках присутствует половинный аргумент при 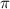$\pi$ , то косинус поменяется на синус, знак будет отрицательным, потому что если считать, что находится в первой координатной четверти, то при вычислении выражения в скобках значение будет в третьей четверти, где обе функции отрицательны.

$\displaystyle cos\bigg (\frac{7\pi}{2}-x \bigg)=cos\bigg (\frac{3\pi}{2}-x \bigg)=-sinx$

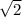
Получаем уравнение $2sinxcosx=-\sqrt{2}sinx$ , которое поделим на $\sqrt{2}$

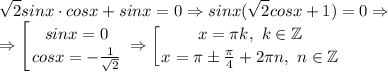
$\displaystyle \sqrt{2}sinx\cdot cosx+sinx=0 \Rightarrow sinx(\sqrt{2} cosx+1)=0 \Rightarrow \\ \Rightarrow \left [ {{sinx=0} \atop {cosx=-\frac{1}{\sqrt{2}} }} \right. \Rightarrow \left [ {{x=\pi k, \ k \in \mathbb{Z}} \atop {x=\pi \pm \frac{\pi}{4} +2\pi n, \ n \in \mathbb{Z}}} \right.$

Первая часть готова, осталось проанализировать каждую серию решений на принадлежность промежутку $\displaystyle \bigg[-\pi; \frac{3\pi}{2}\bigg]$

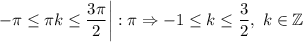
$\displaystyle -\pi \leq \pi k \leq \frac{3\pi}{2} \bigg| : \pi \Rightarrow -1 \leq k \leq \frac{3}{2}, \ k \in \mathbb{Z}$

Здесь подойдут $k=-1; \ k=0: x=\pi \cdot (-1)= -\pi; \ x=\pi \cdot 0 = 0$

Анализируем 2 оставшиеся серии:

$\displaystyle -\pi\leq \pi \pm \frac{\pi}{4}+2\pi n\leq \frac{3\pi}{2} \bigg|:2\pi \Rightarrow -\frac{1}{2}\leq \frac{1}{2}\pm \frac{1}{8}+n\leq \frac{3}{4} \Rightarrow \\ \Rightarrow -1\leq \pm\frac{1}{8}+n\leq \frac{1}{4} , \ n \in \mathbb{Z}$

Здесь уже необходимо рассматривать отдельно.

Первое с "+" возьмем: 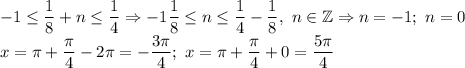$\displaystyle -1 \leq \frac{1}{8}+n \leq \frac{1}{4} \Rightarrow -1\frac{1}{8}\leq n \leq \frac{1}{4}-\frac{1}{8} , \ n \in \mathbb{Z} \Rightarrow n=-1; \ n=0 \\ x=\pi+\frac{\pi}{4}-2\pi=-\frac{3\pi}{4}; \ x=\pi + \frac{\pi}{4} +0=\frac{5\pi}{4}$

В последней серии решений та же логика, просто исходно дробь будет со знаком "-", значит, в обе части двойного неравенства пойдет с "+"

$\displaystyle -\frac{7}{8} \leq n \leq \frac{1}{4} + \frac{1}{8} \Rightarrow n=0 \\ x=\pi - \frac{\pi}{4}+2\pi \cdot 0 = \frac{3\pi}{4}$

Теперь можно записывать ответ:

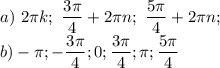
$\displaystyle a) \ 2\pi k; \ \frac{3\pi}{4}+2\pi n; \ \frac{5\pi}{4}+2\pi n; \\ b) -\pi; -\frac{3\pi}{4}; 0; \frac{3\pi}{4}; \pi; \frac{5\pi}{4}$

Переходим к 13. Это неравенство.

Сразу видно, что $25^x-10\cdot 5^x+26$ можно заменить на переменную, и тогда неравенство станет куда проще.

$\displaystyle 25^x-10\cdot 5^x+26=t \Rightarrow t-2+\frac{1}{t} \geq 0 \Rightarrow \frac{t^2-2t+1}{t} \geq 0 \Rightarrow \frac{(t-1)^2}{t}\geq 0$

Если знаменатель больше нуля, то и неравенство будет больше 0. Особый случай - когда числитель равен 1, но 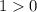, поэтому решением этого неравенство является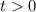

Возвращаемся к замене и решаем относительно :

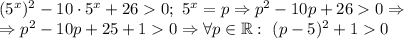
$(5^x)^2-10\cdot 5^x+260; \ 5^x=p \Rightarrow p^2-10p+260 \Rightarrow \\ \Rightarrow p^2-10p+25+10 \Rightarrow \forall p\in \mathbb{R}: \ (p-5)^2+10$

Тогда получается, что и для любого неравенство выполняется.

ответ: 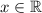$x\in \mathbb{R}$

Решение задачи с параметром прикрепляю отдельным документом, так как мне не хватило ограничения на 5000 символов, к сожалению (

4,7(44 оценок)

Ответ:

Вася2288221

20.10.2021

Объяснение:

Для того, чтобы вычислить площадь фигуры, ограниченной данными линиями, мы сперва должны построить их на графике

Теперь мы видим, что функцией y = 0, наша искомая фигура разбивается на две симметричные. Их площадь будет равна, то есть для того, чтобы вычислить площадь фигуры, нам достаточно найти площадь одной её половины и умножить на "2".

Получается, площадь равна удвоенному интегралу функции х^3 от 2 до 0.

2 * инт (х^3)dx = 2 * (x^4)/4.

Подставляем наши границы "2" и "0": 2 * (x^4)/4 = 2 * ((2^4)/4 - (0^4)/4) = 2 * 4 = 8.

ответ: S фигуры = 8.

4,7(12 оценок)

Это интересно:

Дом-и-сад

30.06.2021

Как повесить полку, не используя для этого гвозди...

Семейная-жизнь

26.12.2020

Правильное питание для мам, кормящих грудью: Как справиться с диетой...