1. Область определения функции: множество всех действительных чисел.
2. Функция не периодическая.
3. Проверим на четность или нечетность функции:
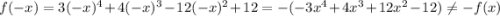
Функция является ни четной ни нечетной.
4. Точки пересечения с осями координат:
4.1. Точки пересечения с осью абсцисс(y=0).
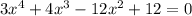 - если сможете решить такое уравнение - вперёд! :) (на графику покажу приближенные значения)
- если сможете решить такое уравнение - вперёд! :) (на графику покажу приближенные значения)
4.2. Точки пересечения с осью ординат(x=0):
Раз х=0, то 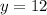
5. Точки экстремума, возрастание и убывает функции.
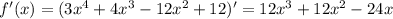
Приравниваем теперь производную функции к нулю, имеем:
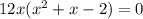
Произведение равно нулю, если хотя бы один из множителей равен нулю.
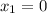
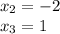
____-___(-2)___+__(0)__-____(1)___+___
Функция возрастает на промежутке 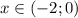 и
и 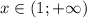 , а убывает -
, а убывает - 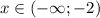 и
и 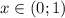 . Производная функции в точке х=-2 и х=1 меняет знак с (-) на (+), значит точка х=-2 и х=1 являются точками локального минимума. А в точке х=0 производная функции меняет знак с (+) на (-), следовательно, точка х = 0 - локальный максимум.
. Производная функции в точке х=-2 и х=1 меняет знак с (-) на (+), значит точка х=-2 и х=1 являются точками локального минимума. А в точке х=0 производная функции меняет знак с (+) на (-), следовательно, точка х = 0 - локальный максимум.
6. Точки перегиба
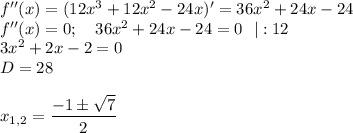
На промежутке 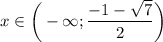 и
и 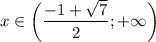 функция выпукла вниз, а на промежутке
функция выпукла вниз, а на промежутке 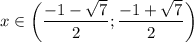 - выпукла вверх.
- выпукла вверх.
Вертикальных, горизонтальных и наклонных асимптот нет.
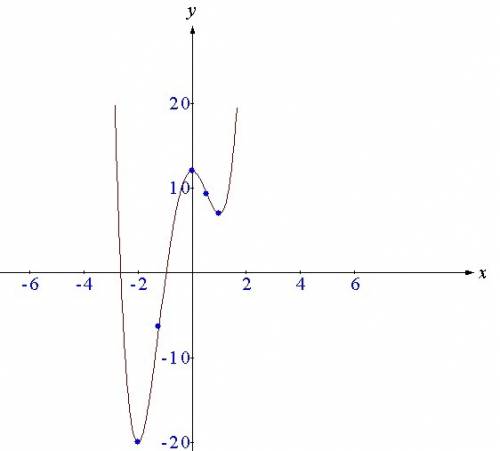
Теперь найдем количество корней f(x)=a для каждого действительно значения параметра а.
f(x)=a - прямая, параллельная оси абсцисс.
При 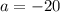 уравнение будет иметь один корень.
уравнение будет иметь один корень.
При 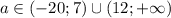 уравнение имеет два корня.
уравнение имеет два корня.
При 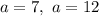 уравнения имеет три корня
уравнения имеет три корня
При 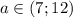 уравнение имеет четыре корня.
уравнение имеет четыре корня.
Составим систему уравнений:
{2х+у=445, |*(-2)
{3х+2у=765
{-4х-2у=-890,
{3х+2у=765
Почленно прибавляем:
-х=-125
х=125
Находим у:
2*125 + у = 445
250 + у = 445
у=445-250
у=195
ответ. 125 рублей стоит детский билет, 195 рублей стоит взрослый билет.