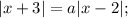 Конечно, решаем графически. Строим график
Конечно, решаем графически. Строим график 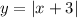 , я думаю, тут легко - смещение на 3 ед. влево по OX, график - "галка". Второй график зависит от параметра и тут рассматриваем
, я думаю, тут легко - смещение на 3 ед. влево по OX, график - "галка". Второй график зависит от параметра и тут рассматриваем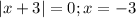 , корень один, подойдёт.
, корень один, подойдёт.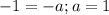 . В итоге получаем, что a=0, a=1. Иначе (a>1) будут 2 точки пересечения
. В итоге получаем, что a=0, a=1. Иначе (a>1) будут 2 точки пересечения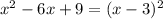 , строим обычную параболу
, строим обычную параболу 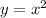 , только сместим её на 3 ед. вправо по OX.
, только сместим её на 3 ед. вправо по OX.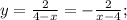 можно построить
можно построить 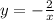 , посчитать несколько значений, потом сместить график на 4 ед. вправо по OX (он до переноса располагался во 2 и 4 четвертях, так как есть знак "-"). Есть красивый корень x=-2
, посчитать несколько значений, потом сместить график на 4 ед. вправо по OX (он до переноса располагался во 2 и 4 четвертях, так как есть знак "-"). Есть красивый корень x=-2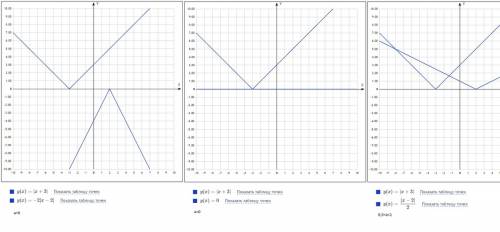
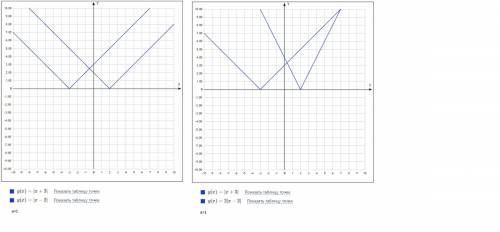
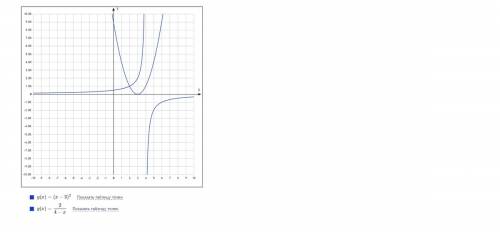
#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
![(x-\frac{3-\sqrt{13}}{2})(x-\frac{3+\sqrt{13}}{2})\geq0 \\\ x \in (-\infty; \frac{3-\sqrt{13}}{2}] \cup [\frac{3+\sqrt{13}}{2}; +\infty)](/tpl/images/0172/7524/775a9.png)
C учётом (-∞;3/2)U[2;6) получим ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ: ![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC => 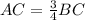
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
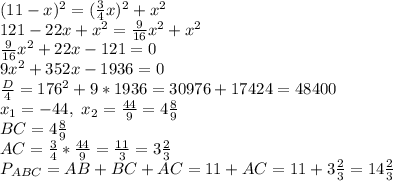
ответ: 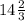
5х - 2у = 0
3х + 2у - 16 = 0
Решим эту систему 3-мя
1. сложения
5х - 2у = 0
+ 3х + 2у - 16 = 0
8х - 16 = 0; 8х = 16; х = 2
подстановки
5х - 2у = 0; 5x = 2y; y = 2,5x
3х + 2у - 16 = 0; 2y = 16 - 3x; y = 8 - 1,5x , т.к. у=у, то
2,5x =8 - 1,5x ; 4x = 8; x=2
3. Графический
5х - 2у = 0 находим точки для этого уравнения
х 0 2
у 0 5
и проводим через точки (0;0) и (2;5) прямую.
Теперь строим 2-й график для уравнения
3х + 2у - 16 = 0
х 0 2
у 8 5
и снова проводим через точки (0;8) и (2;5) вторую прямую.
Эти прямые пересекутся в точке (2;5). Получаем х=2, у=5.