а² – b² = 2017
а² – b² = (а – b) * (а + b)
(а – b) * (а + b) = 2017
Число 2017 простое, поэтому имеет только два натуральных делителя 1 и 2017.
2017 = 1 * 2017
Поэтому
(а – b) * (а + b) = 1 * 2017
Имеем систему
{а + b = 2017
{а – b = 1
Из второго уравнения получим
а = b + 1
Подставим в первое уравнение
(b + 1) + b = 2017
2 b = 2017 - 1
2 b = 2016
b = 2016 : 2
b = 1008
а = 1008 + 1 = 1009
Проверка чисел а = 1009; b = 1008
1009² – 1008² = 2017
1018081 – 1016064 = 2017
2017 = 2017
ответ: существует только 1 вариант натуральных чисел разность квадратов которых равна числу 2017. Это числа 1008 и 1009.
Дана функция
f(x)=4+3·x-x²
1) координаты точек пересечения графика с осью абсцисс:
f(x)=0 ⇔ 4+3·x-x²=0 ⇔ x²-3·x-4=0: D=(-3)²-4·1·(-4)=9+16=25=5²
x₁=(3-5)/(2·1)= -2/2= -1; x₂=(3+5)/(2·1)= 8/2= 4.
ответ: (-1; 0), (4; 0).
2) координаты точек пересечения графика с осью ординат:
f(0)=4+3·0-0²=4
ответ: (0; 4).
3) координаты точек пересечения графика с прямой y=-2·x²+3:
f(x)=y ⇔ 4+3·x-x²=-2·x²+3 ⇔ x²+3·x+1=0 : D=3²-4·1·1=9-4=5
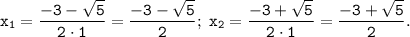
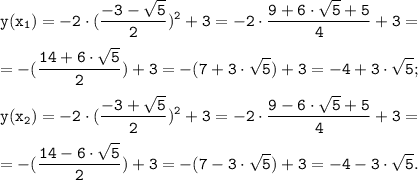
ответ: 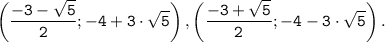
4) наибольшее значение функции:
f(x)=4+3·x-x²=-(x²-3·x-4)=-(x²-2·(3/2)·x+(3/2)²-(3/2)²-4)=
=-(x²-2·(3/2)·x+(3/2)²)+(3/2)²+4=4+9/4-(x-3/2)²=6,25-(x-1,5)²≤ 6,25
Отсюда, если (x-1,5)²=0, то получаем наибольшее значение функции.
ответ: 6,25.
8x+y=-6+5y-12=0
Y-5y+8x=-6-12=0
-4y+8x=-18=0
-4y+8x+18=0
D=64-4*(-4)*18=64+288=352
X1,2=-8^2+корень352:-8
X2=-8^2-корень352:-8