Покажу один из сопособов решения таких неравенств
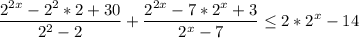
1) проверим ограничения
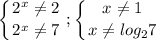
2) введем замену 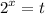
получаем,
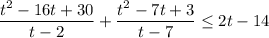
А далее самое интересное
будем делить многочлен на многочлен
_t²-16t+30 | t-2 и _t²-7t+3 | t-7
t²-2t ______ t²-7t _____
_____ t-14 ____ t
_ -14t+30 3 (остаток)
-14t+28
------------
2 (остаток)
тогда
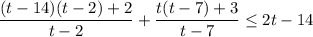
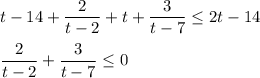
теперь все совсем просто
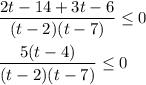
решаем методом интервалов
__-____ 2 ___+____4___-____7___+____
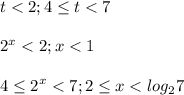
Не забываем проверить ограничение
ответ (-∞; 1)∪[2; log₂7)
fнаиб = 4; f наим = 0
Объяснение:
28б
f(x) = x³ - 6x² + 9x при х ∈ [0; 3]
Значения функции на концах интервала
f(0) = 0
f(3) = 27 - 54 + 27 = 0
Производная функции
f'(x) = 3x² - 12x + 9
Точки экстремумов
3x² - 12x + 9 = 0
х² - 4х + 3 = 0
D = 16 - 12 = 4 = 2²
x₁ = 0.5(4 - 2) = 1
x₂ = 0.5 (4 + 2) = 3
В точке х₁ = 1 находится локальный максимум
f(1) = 1 - 6 + 9 = 4 - максимальное значение
В точке х₂ = 3 находится локальный минимум
f(3) = 0
Сравнивая со значениями функции на границах интервала, делаем вывод. что наибольшее значение функции на заданном интервале равно 4. наименьшее равно 0.