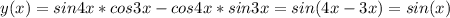
есть 
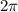
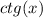равен 
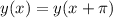
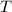- искомый период, тогда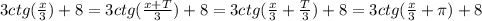
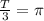
относительно оси OX на 8 единиц вверх, также не влияя на период
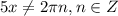
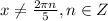
- это симметричное относительно начала координат множество точек,
также симметрична относительно начала координат. Это означает, что есть смысл проверять функцию на парность, дальше.
Поставим перед собой задачу: пусть нам надо решить целое рациональное неравенство с одной переменной x вида r(x)<s(x) (знак неравенства, естественно, может быть иным ≤, >, ≥), где r(x) и s(x) – некоторые целые рациональные выражения. Для ее решения будем использовать равносильные преобразования неравенства.
Перенесем выражение из правой части в левую, что нас приведет к равносильному неравенству вида r(x)−s(x)<0 (≤, >, ≥) с нулем справа. Очевидно, что выражениеr(x)−s(x), образовавшееся в левой части, тоже целое, а известно, что можно любоецелое выражение преобразовать в многочлен. Преобразовав выражение r(x)−s(x) в тождественно равный ему многочлен h(x) (здесь заметим, что выражения r(x)−s(x) иh(x) имеют одинаковую область допустимых значений переменной x), мы перейдем к равносильному неравенству h(x)<0 (≤, >, ≥).
В простейших случаях проделанных преобразований будет достаточно, чтобы получить искомое решение, так как они приведут нас от исходного целого рационального неравенства к неравенству, которое мы умеем решать, например, к линейному или квадратному. Рассмотрим примеры.
cos 2x = 1 - 2sin^2 x
3 - 6sin^2 x - 7sin x - 3√3 = 0
Меняем знаки
6sin^2 x + 7sin x - 3 + 3√3 = 0
Обыкновенное квадратное уравнение относительно sin x
D = 7^2 - 4*6(-3+3√3) = 49+72-72√3 = 121-72√3 ~ -3,7 < 0
Решений нет