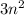 делится на 3, нужно показать еще что
делится на 3, нужно показать еще что  делится на 3
делится на 3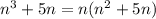
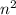 при делении на 3 дает остаток 1, а значит
при делении на 3 дает остаток 1, а значит 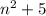 дает остаток при делении на 3 - 0, а значит делится нацело
дает остаток при делении на 3 - 0, а значит делится нацело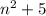 делится нацело на 3, произведение делится на 3, и исходное выражение делится нацело на 3
делится нацело на 3, произведение делится на 3, и исходное выражение делится нацело на 3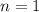 ;
; 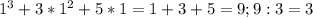
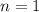
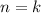
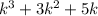 делится нацело на 3.
делится нацело на 3.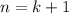
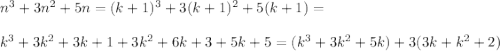 а значит кратное 3 (выражение в первой скобке кратное 3 в силу допущения, во второй один из множителей а именно множитель 3 кратный 3)
а значит кратное 3 (выражение в первой скобке кратное 3 в силу допущения, во второй один из множителей а именно множитель 3 кратный 3)
y=3/4
6 3/4: 5 1/4=27/4*4/21=9/7=1 2/7