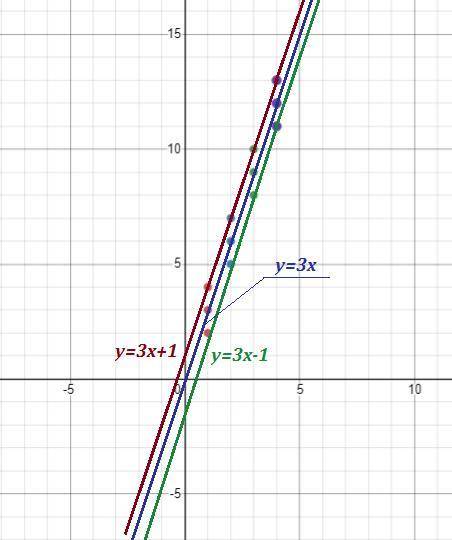
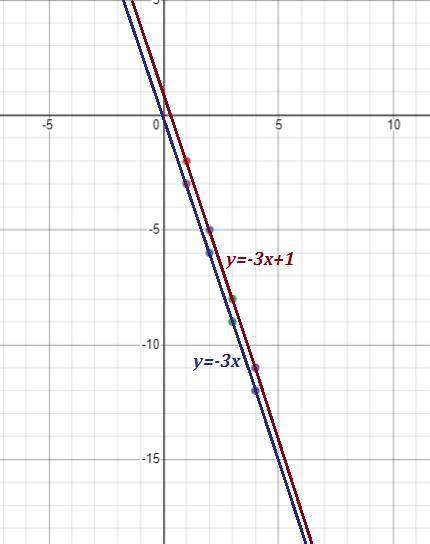
Чтобы с таблицы задать функцию, надо отметить точки на координатной плоскости и постараться увидеть закономерность. Все функции линейные, то есть графики - прямые линии .
1) у=3х , 2) у=3х+1 , 3) у=3х-1 , 4) у=-3х , 5) у=-3х+1 .
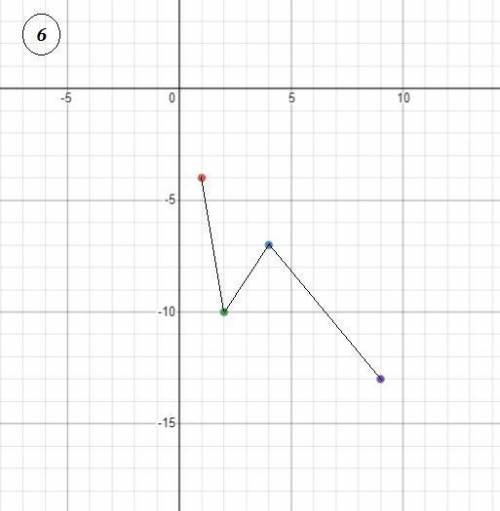
6) Здесь линейной закономерности не просматривается . Если бы в таблице значения "х" бы ли бы 1 , 2 , 3 , 4 , то есть таблица выглядела бы так
х | 1 | 2 | 3 | 4 |
y | -4 | -7 | -10 | -13 | , то функция имела бы вид у= -3х -1 .
В этом задании скорее всего была допущена описка .
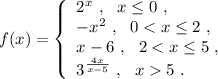
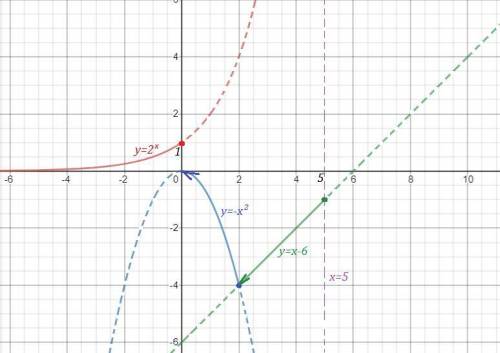
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
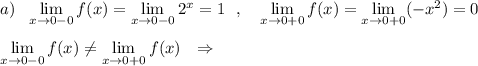
При х=0 функция имеет разрыв 1 рода .
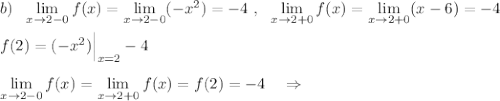
При х=2 функция непрерывна.
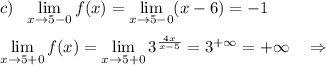
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
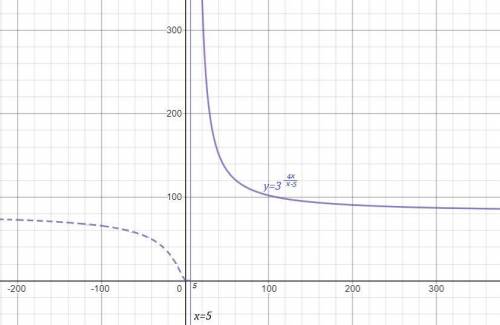
На 1 рисунке нет чертежа функции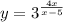 
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
О т в е т. х²+10х+8=0