x²+16=0
х²= -16
х= -+√16
6x²-18=0
6х²=18
х²=3
х=-+√3
Найдите корни уравнений:
x²-3x-5=11-3x
х²-16=0
х²=16
х= -+4
5x²-6=15x-6
5х²-15х=0
х(5х-15)=0
х=0 или 5х=15
х=3
Найдите дискриминант квадратного уравнения:
5x²-4x-1=0
D=16+20=36
x²-6x+9=0
D= 36-36=0
3x-x²+10=0
D=9+40= 49
2x+3+2x²=0
D= 4-48=-44
Сколько корней имеет уравнение:
НАПОМИНАЮ, ЧТО ЕСЛИ ДИСКРИМИНАНТ- ПОЛОЖИТЕЛЬНОЕ ЧИСЛО, ТО УРАВНЕНИЕ ИМЕЕТ 2 КОРНЯ, ЕСЛИ ОТРИЦАТЕЛЬНЫЙ, ТО НЕ ИМЕЕТ КОРНЕЙ. А ЕСЛИ РАВЕН 0, ТО ИМЕЕТ 1 КОРЕНЬ.
6x-5x=0
х=0
один корень
x²-4x+4=0
D= 16-16=0
имеет один корень
3x²-4=0
D=0+48=48
имеет 2 корня
x²-4x+5=0
D= 16-20=-4
не имеет корней
 .
. .
. .
.
 . Но
. Но  фактически лишнее неравенство, оно выполняется автоматически потому, что
фактически лишнее неравенство, оно выполняется автоматически потому, что 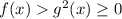 , ибо полный квадрат всегда неотрицателен.
, ибо полный квадрат всегда неотрицателен.
(2sin2βcos2β-2sin2βcos2β)/(cos2β) + 0.29=0+0.29=0.29
2.нужные формулы:sin²x=(1-cos2x)/2 ; cos²x=(1+cos2x)/2
((1-cos(2x/2))-(1+cos(2x/2))/2*√3 все в двойных скобках до /2-числитель дроби,знаменатель 2,вся дробь умножается на √3
=√3(1-cosx-1-cosx)/2=-2√3cosx/2=-√3cosx
-√3*cos5π/6=(-√3)*(-√3)/2=1.5
3.нужная формула:sin²β=1-cos²β
sin²β=1-0.8²=0.36
в указанном промежутке sinβ=-0.6
4.нужная формула:1+tg²x=1/cos²x
1+(24/7)²=1/cos²x
625/9=1/cos²x
cos²x=49/625
в указанном промежутке cosx=-7/25=-0.28
5.нужные формулы:1+сtg²x=1/sin²x sin²x=(1-cos2x)/2
1+(-4/3)²=1/sin²x
sin²x=9/25
9/25=(1-cos2x)/2
18/25=1-cos2x
cos2x=1-18/25=7/25=0.28