Три целочисленные стороны треугольника составляют арифметическую прогрессию :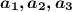 
с разностью d. Тогда
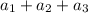=15 см - по условию
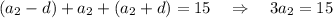
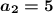см
Разность арифметической прогрессии для сторон треугольника может принимать целые значения от -4 до +4, так как сторона треугольника не может быть равна нулю и быть отрицательной.
Для стационарной (постоянной) арифметической прогрессии :
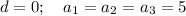см - равносторонний треугольник
Для возрастающей арифметической прогрессии :
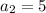см,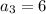 
см, 
см
4 + 5 > 6 - неравенство треугольника выполняется
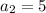см, 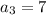см, 
см
3 + 5 > 7 - неравенство треугольника выполняется
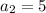см, 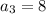см, 
см
2 + 5 < 8 - неравенство треугольника не выполняется
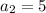см, 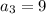см, 
см
1 + 5 < 9 - неравенство треугольника не выполняется
Для убывающей арифметической прогрессии при отрицательных значениях d поменяется порядок сторон ( первая и третья), но числовые значения будут такими же.
ответ : 1) 5 см, 5 см, 5 см; 2) 4 см, 5 см, 6 см; 3) 3 см, 5 см, 7 см
Обозначим а - среднюю сторону треугольника.
Тогда с учетом разности прогрессии d:
а - d - меньшая сторона, а + d - большая сторона
По условию:
(a - d) + a + (a + d) = 15
3a = 15
a = 5 (средняя сторона)
По неравенству треугольника: сумма длин двух любых сторон больше длины третьей стороны:
(а - d) + 5 > a + d
2d < 5
d < 2,5
Так как d может принимать только целые положительные значения, то это могут быть только 1 или 2.
при d = 1: а - d = 4 см; а = 5 см; а + d = 6 см
при d = 2: а - d = 3 см; а = 5 см; а + d = 7 см
ответ: стороны треугольника 4 см; 5 см; 6 см или 3 см; 5 см; 7 см.
2) 5^3=5*5*5 = 125
3) 5^4=5*5*5*5 = 625
4) 5^7=5^4*5^3=625*125 = 78125
5) 5^10=5^7*5^3 = 78125*125 = 9765625
6) 5^15=5^10*5^4*5 = 9765625*625*5 = 30517578125
7) 5^20=5^15*5^4*5= 30517578125*625*5 = 95367431640625