Вероятность определяется как отношение числа благоприятных исходов к общему числу исходов. Всего исходов 12, так как есть 12 номеров.
A — «номер является чётным числом»
Подходящие номера: 2, 4, 6, 8, 10, 12 - 6 номеров
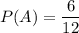
B — «номер делится на 5»
Подходящие номера: 5, 10 - 2 номера
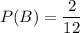
C — «номер делится на 9»
Подходящий номер: 9 - 1 номер
D — «номер меньше или равен 2»
Подходящие номера: 1, 2 - 2 номера
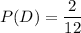
E — «номер больше, чем 2, и меньше, чем 7»
Подходящие номера: 3, 4, 5, 6 - 4 номера
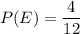
F — «номер является простым числом»
Подходящие номера: 2, 3, 5, 7, 11 - 5 номеров
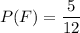
Вероятность того, что из второго ящика переложили в первый ящик стандартную деталь равна 
, то в первом ящике будет 51 деталей из них 19 стандартных. Вероятность того, что извлеченная деталь из первого ящика окажется стандартной равна 
Аналогично, из второго ящика не стандартную деталь переложить в первый ящик можно с вероятностью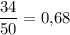 
. Тогда в первом ящике будет 51 деталей из них 18 стандартных. Вероятность того, что из первого ящика выбранная деталь - стандартная, равна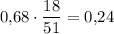 
Искомая вероятность: 
Вторая задача. Число всевозможных исходов равно числу выбрать 4 человек из 6+5=11, т.е. 
из них ищем благоприятные исходы: выбрать 2 мальчика и 2 девочки: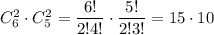 
Искомая вероятность: 
a40= -3 +39*(-3)
a40=-120
S=-3-120/2*40=-2460