В случайном порядке было отобрано 25 студентов экономического факультета и выписан их возраст:
19 17 22 18 17
17 23 21 18 19
17 22 18 18 18
20 17 19 21 17
21 17 18 23 18
Составить статистическое распределение студентов по возрасту. Построить полигон и кумуляту. Найти эмпирическую функцию распределения и дать ее графическое изображение.
Решение. 1. По исходным данным составим статистическое распределение выборки.
Таблица 1.1.
xi
mi
2. Вычислим относительные частоты, и результаты вычислений внесем в третий столбец таблицы 1.2. Относительные частоты находим по формуле
= .
В данном случае объем выборки n=25. Относительные частоты: =7/25=0,28; = 0,28; = 3/25=0,12; = 1/25=0,04; = 3/25=0,12; = =2/25=0,08.
=0,28 + 0,28 + 0,12 + 0,04 + 0,12 + 0,08 + 0,08 = 1.
3. Вычислим накопленные частоты и результаты внесем в четвертый столбец таблицы 1.2.
mx1= m1=7; mx2= m1 + m2=7 + 7=14; mx3= m1 + m2 + m3 =7 + 7 +3=17; mx4= m1 + m2 + m3 + m4=7 + 7 + 3 + 1=18; mx5=7 + 7 + 3 + 1 + 3 = 21; mx6=21 + 2 = 23; mx7= 25.
Вычисленные относительные накопленные частоты указаны в пятом столбце таблицы 1.2.
Таблица 1.2.
варианты xi частоты mi относительные частоты, накопленные частоты, mxi относительные накопленные частоты
0,28 0,28
0,28 0,56
0,12 0,68
0,04 0,72
0,12 0,84
0,08 0,92
0,08
4. Для построения полигона распределения отложим на оси абсцисс варианты xi , на оси ординат – частоты mi.
Рис. 1.1.
Для построения кумуляты отложим на оси абсцисс варианты xi, на оси ординат – накопленные частоты.
Рис. 1.2.
5. Найдем эмпирическую функцию F*(x) по данному распределению выборки.
Объем выборки n=25.
Наименьшая варианта х1=17, следовательно F*(x)=0, при х≤17. Значение х<18, а именно х1=17 наблюдалось 7 раз, следовательно F*(x)=7/25=0,28, при 17<х≤18. Значения х<19, а именно х1=17, х1=18 наблюдались 7+7=14 раз, следовательно F*(x)=14/25=0,56, при 18<х≤19. Аналогично, F*(x)=17/25=0,68 при 19<х≤20; F*(x)=18/25=0,72, при 20<х≤21; F*(x)=21/25=0,84, при 21<х≤22; F*(x)=23/25=0,92, при 22<х≤23. Так как х7=23 – наибольшая варианта, следовательно F*(x)=1, при х >23.
Эмпирическая функция имеет вид
F*(x)=
Построим график этой функции
Рис. 1.3.
Пример 2. Наблюдения за жирностью молока у 50 коров дали следующие результаты (в %).
3,86 3,84 3,69 4,00 3,81 3,73 4,14 3,76
4,06 3,94 3,76 3,46 4,02 3,52 3,72
3,67 3,98 3,71 4,08 4,17 3,89 4,33
3,97 3,57 3,94 3,88 3,72 3,92 3,82
3,61 3,87 3,82 4,01 4,09 4,18 4,03
3,96 4,07 4,16 3,93 3,78 4,26 3,26
4,04 3,99 3,76 3,71 4,02 4,03 3,91
По этим данным построить интервальный вариационный ряд с равными интервалами и изобразить его графически (построить полигон, гистограмму, кумуляту).
Решение. 1. Выполним разбиение данного ряда на интервалы,
n=50, xmax=4,33; xmin=3,46.
Число интервалов к=1 + 3,322lg50=1 + 3,322·1,7=6,6474≈7;
длина каждого интервала h=
за начало первого интервала примем величину хнач=хmin – 0,5h=3,46 – 0,5·0,14=3,46 – 0,07≈3,4.
Таблица 1.3.
жирность молока, интервал середина интервала, хi частота, mi относительная частота, накопленная частота, mxi относительная накопленная частота
3,40- 3,54 3,47 2/50=0,04 0,04
3,54-3,68 3,61 4/50=0,08 6 (2+4) 0,12
3,68-3,82 3,75 13/50=0,26 19 (6+13) 0,38
3,82-3,96 3,89 11/50=0,22 30 (19+11) 0,60
3,96-4,10 4,03 14/50=0,28 44 (30+14) 0,88
4,10-4,24 4,17 4/50=0,08 48 (44+4) 0,96
4,24-4,38 4,31 2/50=0,04 50 (48+2)
2. Для построения гистограммы откладываем на оси абсцисс интервалы длинной h=0,14. На этих интервалах построим прямоугольники высотой, пропорциональной частоте. Для построения полигона середины верхних оснований соединим ломаной линией.
Рис. 1.4.
Для построения кумуляты на оси абсцисс отложим середины интервалов, а на оси ординат – накопленные частоты.
Рис. 1.5.
Объяснение:
max {k / S(k)} = 1 000 000
Объяснение:
Цифра в старшем разряде не может быть равна 0, потому что в противном случае число не будет семизначным. Сначала рассмотрим случай, когда это единственная ненулевая цифра в числе k:
Теперь предположим, что в числе есть другие ненулевые цифры и покажем, что в этом случае значение дроби меньше 10⁶. Цифры числа k обозначим через a₆, a₅, ..., a₀.
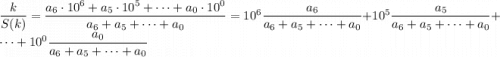
Рассмотрим дробь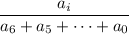 
, где 
– одна из цифр числа k. Заметим, что 
для любых x>0 и y≥0. Тогда если мы оставим в знаменателе этой дроби только два слагаемых, одно из которых (ai) присутствует в числителе, а второе (aj) не равно нулю, будет верно неравенство:
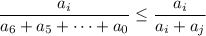
Если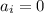 
, то 
. В противном случае мы можем поделить числитель и знаменатель дроби на : 
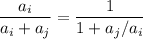, а поскольку ai и aj – это некоторые отличные от нуля цифры, максимально возможное значение этой дроби достигается при ai=9 и aj=1: 
.
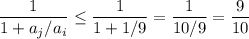Из этого следует, что 
.
Теперь вернемся к исходному отношению k/S(k) при наличии хотя бы двух отличных от нуля цифр:
Таким образом, мы доказали, что максимальное значение дроби k/S(k) равно 10⁶ = 1000000 и достигается, когда все все цифры числа k, кроме первой, равны нулю.
ответ:-3;-2;2