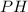сложности или просто задача не решаемая за полинамиальное время , тем самым относится к категорий 
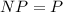классу , это значит что нет такого алгоритма так что он решал бы данную задачу при скажем так рекурсивного метода , ИМЕННО метода ,потому что перебор идет " с отсевом заведомо неоптимальных ветвей" , это видно из-за времени , на просчитание ходов 
- секунда , вы делайте шаг , и теперь Компьютер оценивает ваш ход перебирая остальные , и сужая тем самым последующие ходы в зависимости как вы пойдете в следующий раз , то есть можно это изобразить в виде ГРАФА , на который поставлены приоритеты в зависимости как вы ходили , компьютер описывает все действия при некой функций (но сам принцип , есть оценивание этих самым ветвей графа), которое интерпретируется в сам процессоров в виде битов , вопрос есть ли или существует алгоритм при которой компьютер без проигрышна вас обыграет , то какой он 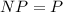, то есть подставив ваши исходные данные в псевдоокоде , есть ли он такой алгоритм который бы решал , данную задачу за некоторое время , ответ
x^2-2x-x^2+6x-9=0
4x=9
x=2.25