Ремарка:
в большинстве случаев использовалась расширенная теорема Виета, которая есть не что иное как счелканье уравнений как семечек в уме. Я рекомендую вам изучить очень хорошо метод переброски, который, поверьте моему опыту, упросить вам жизнь.
Объяснение:
1)

2)
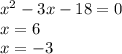
3)
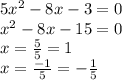
4)
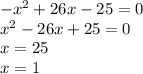
5)
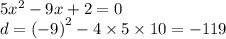
То есть уравнение корней не имеет, так как дискриминант отрицательный.
6)
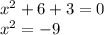
Уравнение корней не имеет, так как какое бы мы число к квадрату не поднесли, результат всегда будет положительный, а не отрицательный, как вот (-9).
7)
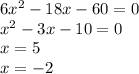
8)
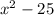
Если задача стоит разложить на множители, то имеем:
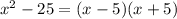
Если задача стоит найти корни уравнения, то имеем:
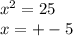
9)
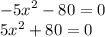
Уравнение не имеет корней, так как левая часть всегда > 0, а не равна ему. Действительно, какое бы мы число не подставили вместо x, оно всегда будет ≥ 80.
10)
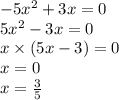
11)
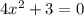
Уравнение не имеет корней, аналогичная ситуация как в уравнении 9.
12)
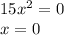
Если даны три стороны, то можно найти углы треугольника по теореме косинусов.
Пусть a=6; b=25; c=29
b²=a²+c²-2·a·c·cos∠B
25²=6²+29²-2·6·29·cos∠B
cos∠B=(36+841-625)/(12·29)=21/29
BD=BC·cos∠B=6*(21/29)=126/29
По теореме Пифагора из Δ BCD высота СD
CD²=BC²-BD²=6²-(126/29)²=36-(15876/841)=14400/841
CD=120/29
( можно найти sin∠B) и
тогда
CD=BC·sin∠B
Второй
Найти площадь по формуле Герона:
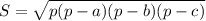
p=(a+b+c)/2 - полупериметр треугольника.
p=(6+25+29)/2=30
p-a=30-6=24
p-b=30-25=5
p-c=30-29=1
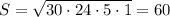
Наименьшая высота проведена к наибольшей стороне.
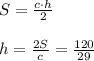
2 - 3х ≠ 0
3х ≠ 2
х ≠ 2/3
2) у = arcSin(x² + 2) учитываем, что значения синуса - это [-1;1]
x² + 2 - это положительное число >1
ответ: данная функция не определена
3)у = (4х -2)/√(4 + 2х²) Учитываем, что :
а) делить на 0 нельзя,
б) под корнем должно стоять неотрицательное число
2х² + 4 ≠ 0
2х² + 4 > 0
ответ: х - любое