Кол-во таких чисел=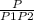 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 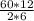 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
Кол-во таких чисел=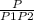 .
.
Здесь P -общее кол0во перестановок 6 чисел : P=6!=60*12
P1 - число перестановок цифры 1 в этом числе. То есть мы как бы путем деления общего числа перестановок на число перестановк конкретной цифры убираем повторяющиеся перестановки, образуемые этой цифрой. Так как кол-во единиц в наборе 2 штуки, то
P1=2!=2
Аналогично для P2=3!=6
P= 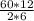 =60.
=60.
если бы например в наборе были бы только единицы напрмиер, то получилось бы единственное возможное число, что доказывает некоторую универсальность моей формулой
x²+(-x)²+4x+4x=0⇒2x²+8x=0⇒2x(x+4)=0⇒x₁=0; x₂=-4
итак, точки пересечения: A(0;0), B(-4;4)
cоставим систему уравнений, подставив в общее уравнение окружности
(x-a)²+(y-b)²=r₂ координаты точек A, B, M₁
(0-a)²+(0-b)²=r₂
(-4-a)²+(4-b)²=r²
(4-a)²+(4-b)²=r²
отнимем от второго уравнения третье
a²+b²=r²
(4+a)²-(4-a)²=0⇒16+8a+a²-16+8a-a²=0⇒16a=0⇒a=0
подставим во все уравнения a=0
b²=r²
16+(4-b)²=r²
16+(4-b)²=r²
подставим во второе уравнение r²=b²
b²=r²
16+16-8b+b²=b²⇒32-8b+b²-b²⇒8b=32⇒b=4
имеем решение системы a=0; b=4; r=4
уравнение окружности x²+(y-4)²=4²