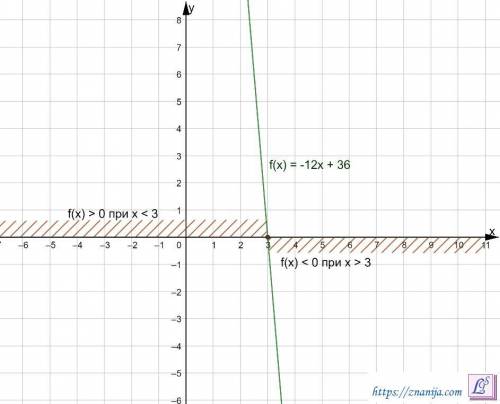
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
Функция f(x) = -12x + 36 убывающая.
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
Объяснение:
f(x) = -12x + 36
Это линейная функция, ее график прямая линия. Общий вид линейной функции f(x) = kx + b.
Коэффициент k определяет угол наклона прямой к оси ОХ.
k = -12, k < 0, прямая проходит через II - IV четверти. (k < 0, угол между прямой и положительный направлением оси ОХ тупой)
⇒ Функция f(x) = -12x + 36 убывающая.
f(x) = 0; -12x + 36 = 0; 12x = 36; x = 3
f(x) = 0 при x = 3.
f(x) > 0 при x ∈ (-∞; 3)
f(x) < 0 при x ∈(3; +∞)
y ' = [(4x+12)'*(x+2)^2 - (4x+12)*((x+2)^2)'] / (x+2)^4=
=[4(x+2)^2 -(4x+12)(2(x+2))] / (x+2)^4=
=(4x^2+16x+16-8x^2-40x-48)/(x+2)^2=
=(-4x^2-24x-32)/(x+2)^4
Приравняем производную к нулю:
(-4x^2-24x-32)/(x+2)^4=0
-4x^2-24x-32=0
Разделим обе части уравнения на "-4":
x^2+6x+8=0
D=6^2-4*1*8=4
x1=(-6-2)/2=-4
x2=(-6+2)/2=-2
Производная не существует в точке х=-2. Это точка разрыва функции(полюс).
+-4--2+
max.
Итак: на луче ( -беск.: -4] функция возрастает; на полуинтервале
[-4;-2) - убывает, а на промежутке (-2;+беск.) - возрастает.
Х=-4 - точка максимума, причем У max. = -1(подставили значение х=-4 в первоначальную формулу).