Question

Решите неравенство -3(х+8)(х-5)< 0

Answer 1

делишь выражение на -3.

(х+8)(х-5)>0

 Чертишь координатную прямую:

+-+___> 

          -8                5

В ответ пишешь интервалы где стоит знак +

( минус бесконечность; -8) и (5; плюс бесконечность) 

Элементарно Ватсон!) 

Answer 2

-3(x^2-5x+8x-40)<0;

-3(x^2+3x-40)<0;

-3x^2-9x+120<0;

(чтобы с минусами не запутаться можно всё неравенство на -1 умножить, тогда знки все поменяются и знак "<" станет ">")

3x^2+9x-120>0;

(так же число 3;9 и 120 деляться на 3, можно тем самым разделить всё на 3 и получить неравенство более лёгкое)

x^2+3x-40>0;

D(дискриминант)=b^2-4ac=9-4*1*(-40)=9+160=169;

x1=-b+корень(D)/2a=-3+13/2=5

x2=-b-корень(D)/2a=-3-13/2=-8

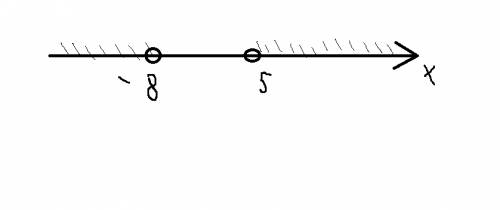
рисуешь координатную прямую и отмечаешь эти точки и промежуток (>) b точки пустые т.к. знак строгий...

ответ:(-бесконечности; -8)U(5;+бесконечности)