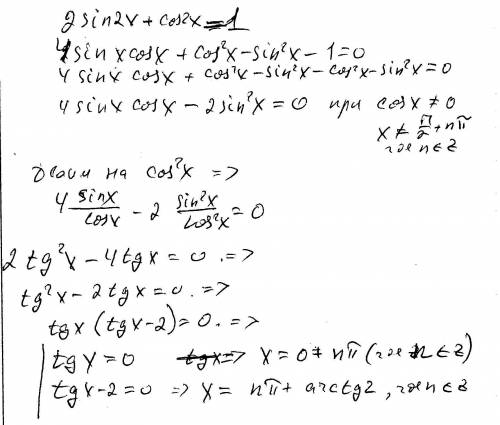
4sinx cosx + cos^2 x-sin^2 x = cos^2 x+sin^2 x
4 sinx cosx +cos^2 x-sin^2 x-cos^2 x-sin^2x = 0
4sinxcosx-2sin^2 x=0
2sinx(2cosx-sinx)=0
sinx =0 или 2cosx-sinx=0
x=пn 2ctgx-1=0 (разделили всё на sinx)
ctgx=1/2
x=arcctg1/2 +пn
ответ: пn; arcctg1/2+пn
ответ: 10 .
объяснение:
область определения функции cos - всё множество действительных чисел, а вот множество значений этой функции (вне зависимости, какой аргумент будет записан) - это отрезок от (-1) до (+1) .
при возведении в квадрат все отрицательные числа становятся положительными, поэтому
получили множество значений заданной функции - это сегмент [0,4] .
целые числа из сегмента [0,4] - это 0, 1 , 2 , 3 , 4 .
сложим их (в условии такое ):
0+1+2+3+4=10 .
ответ: 10 .