В решении.
Объяснение:
З двох пунктів, відстань між якими дорівнює 33 км, вирушили одночасно назустріч один одному двоє велосипедистів і зустрілися через 1,5 год. З якою швидкістю їхав кожний велосипедист, якщо для подолання всієї відстані між пунктами одному з них потрібно на 33 хв більше, ніж другому?
Из двух пунктов, расстояние между которыми равно 33 км, отправились одновременно навстречу друг другу два велосипедиста и встретились через 1,5 часа. С какой скоростью ехал каждый велосипедист, если для преодоления всего расстояния между пунктами одном из них нужно на 33 минут больше, чем другому?
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - скорость первого велосипедиста.
у - скорость второго велосипедиста.
х + у - общая скорость велосипедистов.
33/х - время первого велосипедиста на всё расстояние.
33/у - время второго велосипедиста на всё расстояние.
По условию задачи система уравнений:
(х + у) * 1,5 = 33
33/х - 33/у = 33/60 = 11/20 (сократить на 3)
В первом уравнении раскрыть скобки, а все части второго уравнения умножить на 20ху, чтобы избавиться от дроби:
1,5х + 1,5у = 33
20у*33 - 20х*33 = ху*11
Первое уравнение разделить на 1,5 для упрощения:
х + у = 22
660у - 660х = 11ху
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х = 22 - у
660у - 660(22 - у) = 11у(22 - у)
660у - 14520 + 660у = 242у - 11у²
Перенести всё в левую часть уравнения и привести подобные:
1320у - 14520 - 242у + 11у² = 0
11у² + 1078у - 14520 = 0
Разделить уравнение на 11 для упрощения:
у² + 98у - 1320 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 9604 + 5280 = 14884 √D=122
у₁=(-b-√D)/2a
у₁=(-98-122)/2 = -220/2 = -110, отбросить, как отрицательный.
у₂=(-b+√D)/2a
у₂=(-98+122)/2
у₂=24/2
у₂=12 (км/час) - скорость второго велосипедиста.
х = 22 - у
х = 10 (км/час) - скорость первого велосипедиста.
Проверка:
33/10 - 33/12 = 3,3 - 2,75 = 0,55 (часа);
0,55 * 60 = 33 (минуты), верно.
Шанс получить в конце 324, 184 или 696 есть только в случае, когда ни одно из перемножаемых чисел не делится на 5 (иначе последняя цифра была бы нулем). Поэтому нужно проанализировать только произведение (5n+1)(5n+2)(5n+3)(5n+4).
Сначала поставим несколько экспериментов.
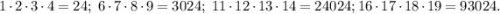
естественно выдвинуть гипотезу, что на конце такого произведения всегда будут цифры 024. Докажем ее.
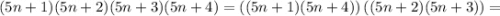
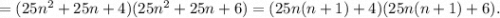
Поскольку n(n+1) является произведением двух соседних натуральных чисел, оно является четным числом: n(n+1)=2k, поэтому получившееся произведение можно записать в виде
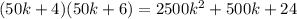
Это доказывает, что две последние цифры - это 2 и 4, но мы замахнулись на более тонкий результат. Имеем:
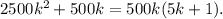
Если k - четное число, то все произведение делится на 1000. Если k - нечетное число, 5k+1 - четное число, и снова все произведение делится на 1000.
Вывод: произведение последовательных натуральных чисел не может заканчиваться ни на 324, ни на 184, ни на 696.
Замечание. Если вопрос был бы только про 324, все это исследование не потребовалось бы, поскольку среди четырех последовательных чисел обязательно найдутся четное число и отличное от него число, делящееся на 4, поэтому их произведение обязательно делится на 8. А вот число, оканчивающееся на 324, на 8 не делится.