ответ: 1) -0,6; -0,4; 2) -10/3;х=-3; 3)Ни при каких; 4)Ни при каких;
Объяснение:
1) (5x+3)^2 =5x+3
(5x+3)^2 -(5x+3)=0
(5x+3)×(5x+3-1)=0
(5x+3)×(5x+2)=0
5x+3=0 либо 5x+2=0
х=-0,6 либо х=-0,4
2) (3x+10)^2 =3x+10
(3x+10)^2 -(3x+10)=0
(3x+10)×(3x+10-1)=0
(3x+10)×(3x+9)=0
3x+10=0 либо 3x+9=0
х=-10/3 либо х=-3
3) (3x-8)^2 =3x^2 - 8x
9х²-48х+64-3x^2 + 8x=0
6х²+ 8x+16=0
3х²+ 4x+8=0
D=4²-4×3×8=-80<0 - уравнение не имеет корней
ответ: Ни при каких
4) (4x+5)^2 =5x^2 +4x
16х²+40х+25-5х²-4х=0
11х²+36х+35=0
D=36²-4×11×35=1296-1540=-244<0 - уравнение не имеет корней
ответ: Ни при каких
Объяснение:
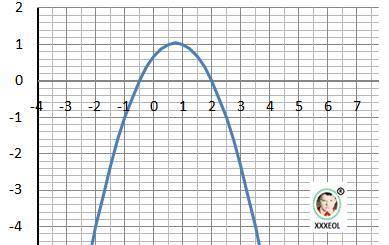
ДАНО: y = - 2/3*x² + x + 2/3 - функция.
1) Область определения - непрерывная гладкая.
D(x) = R = (-∞;+∞)
1) Нули функции: Y(x) = 0. Решаем квадратное уравнение.
х1 = -0.5 и х2 = 2
2) Пересечение с осью ОУ. Y(0) = 2/3.
3) Интервалы знакопостоянства.
Отрицательна: x = (-∞;-0,5)∪(2;+∞)
Положительна между нулями: х =[-0,5;2].
4) Функция общего вида, ни чётная ни нечетная.
5) Поиск экстремов по первой производной.
Y'(x) = - 4/3*x + 1 = 0
x = 3/4 - корень производной
6) Экстремум: максимум Ymax(0.75) = 1.
7) Возрастает: х = (-∞;0.75), убывает х = (0.75;+∞).
8) Точек перегиба нет.
Выпуклая - "горка" - во всей области определения.
Рисунок с графиком в приложении.