Question

1) ∫(x+1)(5x-3)dx 2)∫x^2/√1-x^2dx 3) ∫dx/3√9x-7 в 1 вычислить интеграл методом непосредственного интегрирования , 2 и 3 вычислить интеграл методом подстановки ( замены переменной) заранее 15 , 5 за каждое , заранее

Answer 1

$1)\quad \int (x+1)(5x-3)dx=\int (5x^2+2x-3)dx=\frac{5x^3}{3}+x^2-3x+C\\\\2)\quad \int \frac{x^2\, dx}{\sqrt{1-x^2}} =[\, x=sint,\; dx=cost\, dt,\; t=arcsinx\, ]=\\\\=\int \frac{sin^2t\cdot cost\, dt}{\sqrt{1-sin^2t}} =\int \frac{sin^2t\cdot cost\, dt}{ \sqrt{cos^2t} } =\int \frac{sin^2t\cdot cost\, dt}{cost} =\int sin^2t\, dt=\\\\=\int \frac{1-cos2t}{2} dt=[\, \int cos(kx+b)dx=\frac{1}{k}sin(kx+b)+C\, ]=$

$=\frac{1}{2}t-\frac{1}{2}\cdot \frac{1}{2}sin2t+C=\frac{1}{2}t-\frac{1}{4}\cdot 2sint\cdot cost+C=$

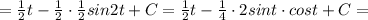
$=\frac{1}{2}arcsinx+\frac{1}{2}sin(arcsinx)\cdot cos(arcsinx)+C=\\\\=\frac{1}{2}arcsinx+\frac{1}{2}\cdot x\cdot \sqrt{1-x^2}+C\\\\3)\quad \int \frac{dx}{3\sqrt{9x-7}} =[\, t=9x-7,\; dt=9dx,\; dx=\frac{dt}{9}\, ]=\\\\=\int \frac{dt}{9\cdot 3\sqrt{t}} =\frac{1}{27}\cdot 2\sqrt{t}+C=\frac{2}{27}\cdot \sqrt{9x-7}+C$