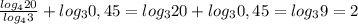
ответ: 30 часов.
Объяснение:
Производительность двух труб равна 1/12 части резервуара за час
Пусть время наполнения первой трубы равно х часов.
Тогда время наполнения 2 трубы равно х +10 часов. соответственно их производительности равны 1/х и 1/х+10 часть/ час.
Совместная производительность равна
1/х + 1/(х +10) = 1/12;
12(х+10) + 12х = х(х+10);
12х +120 +12х =х²+10х;
х² - 24х+10х -120 =0;
х² -14х-120=0;
х1= 20; х2= -6 - не соответствует условию
х=20 часов заполняет 1 труба.
х+10=20+10=30 часов - время заполнения 2-й трубой.
Проверим:
1/20 + 1/30 = (3+2)/60 = 5/60 = 1/12. Всё верно!
Два фермера, работая вместе, могут вспахать поле за 25 часов.
Производительность труда у первого и второго относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?
Пусть Х-производительность 1-го, У-производительность 2-го.
Система:
х+у=125
2х=5у
Последовательно:
2х+2у=2/25
2х-5у=0
7у=2/25 и у=2175
Тогда х=135
Итак, производительности мы нашли.
Поочередно фермеры работали 45,5 часа = 91/2 часа.
Пусть из этого времени 2-ой работал Т часов, тогда 1-ый работал 912-Т часов.
Уравнение:
(91/2-Т)⋅(1/35)+Т⋅(2/175)=1
имеет корень Т=17,5
Проверка.
1. проверим , что х+у=125
1/35+2/175=(70+175)/(175⋅35)=7/175=1/25
2. проверим, что 2х=3у:
2/35=5⋅2/175
3. Проверим уравнение при поочередной работе:
Если 2-ой работал 17,5 часов, то 1-ый работал 45,5-17,5=28 часов
28⋅135+(352)⋅(2175)=28/35+1/5=1
ОТВЕТ: 17,5