Решить неравенства:
1)
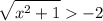
определим ОДЗ:
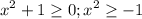
т.е. неравентсво определено на всем множестве R
Подкоренное выражение всегда ≥0. А значит решением данное неравенства будет множество R
ответ: x∈R
2)
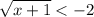
определим ОДЗ:
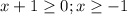
Значит неравенство имеет смысл если х∈[-1;+∞)
Но при этом √x+1 ≥0 и ни когда не будет отрицательным числом, а значит неравенство не выполнимо
ответ: x∈∅
3)
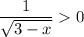
определим ОДЗ:
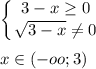
При допустимых х выражение √3-x>0; и значит дробь тоже принимает положительные значения
ответ: x∈(-∞;3)
4)
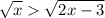
определим ОДЗ:

значит допустимые значения х∈[1.5; +∞)
т.к. с обеих сторон стоят положительные числа то можем данное неравенство возвести в квадрат

по решению х<3
совместим с ОДЗ
ответ: x∈[1.5; 3)
x=998
-5/(998+2)=-5/1000
x=-0,005