2sin2x + 3sinxcosx - 3cos2x = 1;
Представим 1 в виде суммы по основному тригонометрическому тождеству:
sin2x + 3cosxsinx - 3cos2x = sin2x + cos2x;
Приведем подобные:
sin2x + 3cosxsinx - 4cos2x = 0;
Разделим каждый член уравнения на cos2x:
tg2x + 3tgx - 4 = 0;
Произведем замену и решим квадратное уравнение:
t2 + 3t - 4 = 0;
D = 9 + 16 = 25;
t = (-3 +- 5)/2;
t1 = -4, t2 = 1;
Сделаем обратную замену:
tgx = 1; x = pi/4 + pin, n из Z;
tgx = -4; x = arctg(-4) pin, n из Z.
ответ: pi/4 + pin, n из Z; arctg(-4) pin, n из Z.
Объяснение:
Оцени!
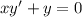
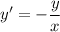 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными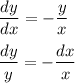
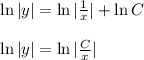
 - общее решение
- общее решение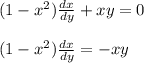

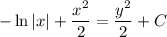 - общий интеграл
- общий интеграл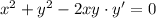

 , тогда
, тогда 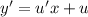



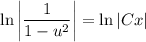
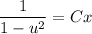
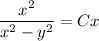 - общий интеграл
- общий интеграл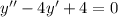
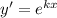 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
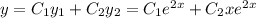 - общее решение
- общее решение
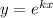 , тогда получаем
, тогда получаем
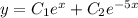

 - частное решение
- частное решение
Х-Ха У-Уа
Хв-Ха = Ув-Уа
(х-1)/(-1-1) = (у-0)/(2-0),
(х-1)/-2 = у/2.
у = к* х + в
Кав = (Ув-Уа)/(Хв-Ха) = 2/-2 = -1.
у = -х + 1.
2) Находим длины сторон:
АВ = √((Хв-Ха)²+(Ув-Уа)²) = √8 2.828427125.
BC = √((Хc-Хв)²+(Ус-Ув)²) = √32 = 5.656854249.
AC = √((Хc-Хa)²+(Ус-Уa)²) = √40 = 6.32455532.
По формуле Герона находим площадь треугольника:
Можно площадь найти по координатам вершин:
Площадь треугольника S=(1/2)*|(Хв-Ха)*(Ус-Уа)-(Хс-Ха)*(Ув-Уа)| = 8.
Длина высот АД = 2S/ВС = 2*8/5.656854249 = 2.828427.
3) Основания медиан (точки пересечения медиан со сторонами).Е(Хв1;Ув1) = (Ха+Хс)/2; (Уа+Ус)/2
Е (-2; -1).
BЕ = √((Хв1-Хв)²+(Ув1-Ув)²)) = 3.16227766.
4) Треугольник - прямоугольный:
УГЛЫ ТРЕУГОЛЬНИКА Угол BAC при 1 вершине A: в радианах = 1.10714871779409 в градусах = 63.434948822922 Угол ABC при 2 вершине B: в радианах = 1.5707963267949 в градусах = 90 Угол BCA при 3 вершине C: в радианах = 0.463647609000806 в градусах = 26.565051177078.
Поэтому точка пересечения высот треугольника ABC это точка В.