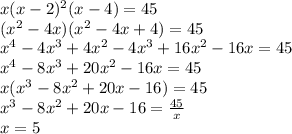
№1 (ответ на фото)
Квадратным уравнением называют уравнение вида ах²+bх+с=0, где коэффициенты а, b, с - любые действительные числа, причём, а≠0. Коэффициенты а, b, с, различают по названиям: а - первый или старший коэффициент; b - второй или коэффициент при х; с - свободный член, свободен от переменной х
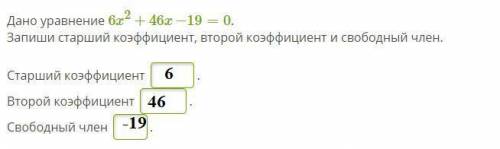
№2 ( ответ на фото)
Приведенное квадратное уравнение – уравнение вида , первый коэффициент которого равен единице
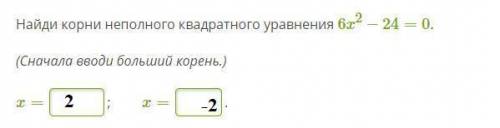
№3.
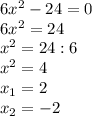
ответ: ±2
№4.
8x²+6x+9=0
a=8 b=6 c=9
D=b^2-4ac=6^2-4*8*9=36-288=-252
№5
x²+14x-8=0
D=14²-4*1*(-8)=196+32=228
√D=√228=2√57
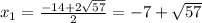
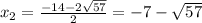
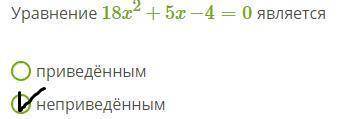


1. y=2x+1.
2. y= -0,5x+1,5.
3. y=5x+10.
Объяснение:
Три прямые являются графиками линейных функций, которые имеют формулу вида y=kx+b.
1) y=kx+b
а) Обратим внимание на точку пересечения с осью Ок. Её координаты (0; 1). При подстановке их в формулу получим
1=k•0+b
b=1, тогда y=kx+1.
б) Теперь выберем на графике ещё одну точку. Желательно, чтобы её координаты были бы целыми числами. В нашем случае это может быть точка (1;3). Подставим и её координаты в формулу:
y=kx+1
3=к•1+1
к = 2.
в) Запишем окончательный ответ: y=2x+1.
Аналогично выполним и другие задания.
2)
а) (0;1,5) принадлежит графику. При подстановке координат в формулу получим
1,5=k•0+b
b=1,5, тогда y=kx+1,5.
б) точка (3;0) принадлежит графику. Подставим и её координаты в формулу:
у=kx+1,5
0=к•3+1,5
3к = -1,5
к = - 0,5.
в) Запишем окончательный ответ: y=-0,5x+1,5.
3)
а) (0;10) принадлежит графику. При подстановке координат в формулу получим
10=k•0+b
b=10, тогда y=kx+10.
б) точка (2;20) принадлежит графику. Подставим и её координаты в формулу:
у=kx+10
20=к•2+10
2к = 10
к = 5.
в) Запишем окончательный ответ: y=5x+10.